Sampling in a nutshell#
In practice, we do not have an infinite collection of sinusoids, endless signals, or unlimited processing time. Instead, signals are sampled over a finite period and stored in discrete form in computer memory. Likewise, the sinusoids used in Fourier analysis are precomputed, finite in number, of limited duration, and represented in discrete form. These practical constraints naturally lead us to the topic of sampling.
Sampling is the process of converting an analog (continuous) signal into a digital (discrete) signal. This conversion is carried out by an Analog-to-Digital Converter (ADC).
The choice of sampling parameters is a critical decision in system design, balancing the need for accurate signal representation with system constraints, application-specific requirements, and price. Poor decisions regarding these sampling parameters can lead to signal distortion, inefficient resource use, and system failure in the worst cases. Therefore, careful consideration and analysis are essential to ensure that the system functions optimally, delivering accurate results within the constraints of available resources.
This section offers only the essential definitions of sampling necessary for understanding the Fourier Transform algorithm and to work through the associated examples. I plan to delve much deeper into the topic of sampling, including its principles, trade-offs, implications, and applications, in a dedicated chapter later in this text.
Sampled signal#
When a continuous signal is sampled, it is captured at equally spaced intervals, converting a smooth, analog waveform into a series of discrete points. This transformation is fundamental in digital signal processing, allowing the continuous signal to be stored, manipulated, and analyzed using digital systems. The figure below illustrates a continuous sinusoidal signal with a frequency of 1Hz, showcasing its smooth, periodic nature.

In the subsequent figure, the 1Hz continuous signal is sampled at eight equally spaced intervals over one period \( T \). The sampling interval, denoted as \( t_s \), is 0.125 seconds. This interval represents the time between consecutive samples.
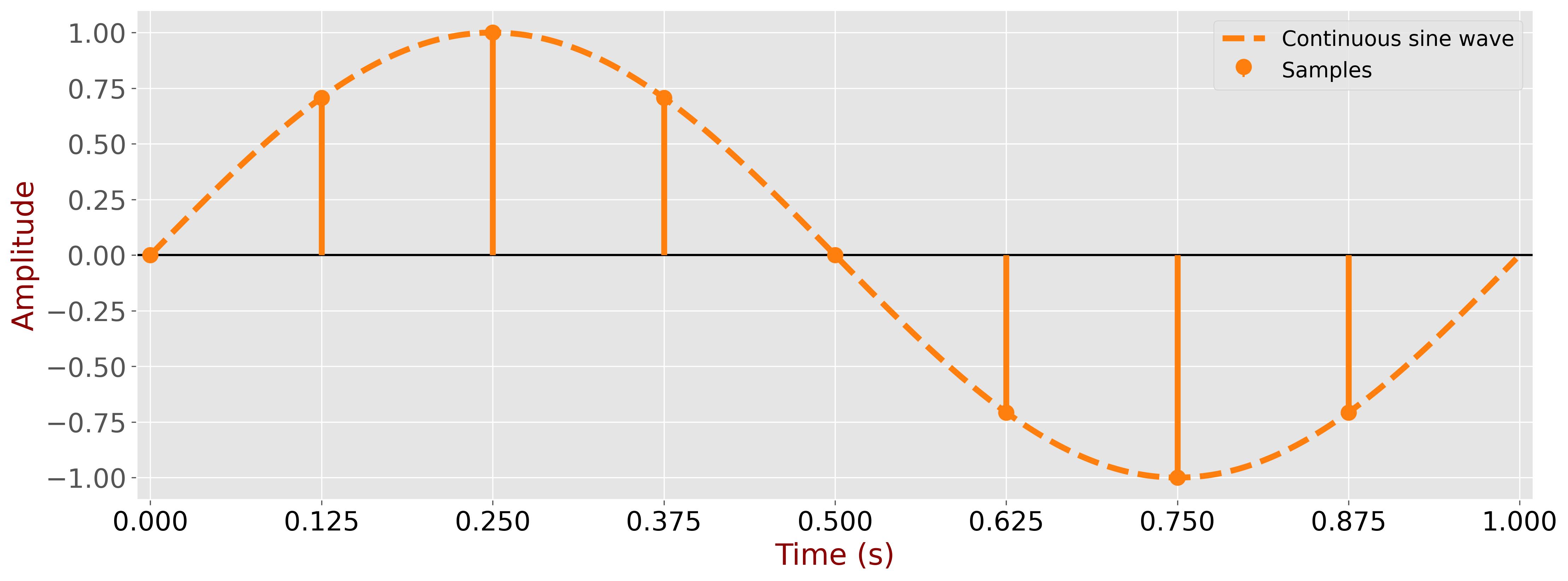
Once sampled, these discrete values are stored digitally in memory. The following figure presents these samples as a function of the sample number \( n \), emphasizing the transition from a continuous to a discrete representation.
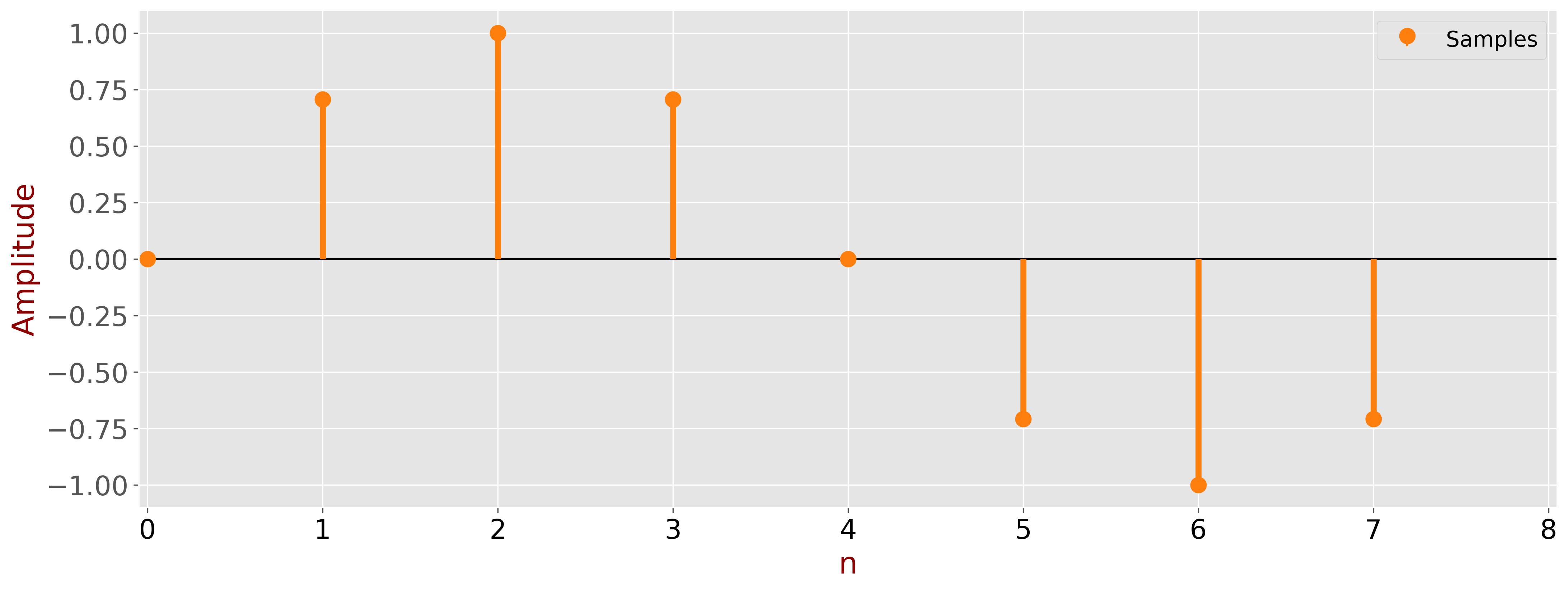
In the realm of discrete signal processing, the concept of time becomes abstract. Whether a 1Hz signal is sampled at intervals of 0.125 seconds, a 1kHz signal at intervals of 0.125 milliseconds, or a 1MHz signal at intervals of 0.125 microseconds, the resulting discrete values will be identical. This illustrates a key principle: in discrete processing, only the sample numbers are significant - time, as a continuous variable, is not explicitly considered.
For example, the Digital Fourier Transform (DFT), a fundamental tool in signal processing, analyzes the frequency components of a discrete signal but does not include a time variable in its equation. Instead, the DFT operates purely on the sequence of samples. This absence of a time variable further underscores that in discrete processing, the focus shifts away from time and toward analyzing the signal’s sample values.
However, to reconstruct the discrete signal back into its continuous form, it is essential to remember the sampling interval \( t_s \). This interval determines the relationship between the sample points and real-world time.
The time associated with a specific sample can be calculated using the formula:
\[ t_n = n t_s \]where \( t_n \) is the time of the \( n \)-th sample.
The sampling frequency \( f_s \), which is the rate at which samples are taken, is defined by the equation:
\[ f_s = \frac{1}{t_s} \]The total sampling period duration \( T \) is given by:
\[ T = N t_s \]where \( N \) represents the number of samples collected.