Periodic Frequencies#
This subsection is crucial for understanding the Discrete Fourier Transform (DFT), providing a foundation for grasping its concepts.
Let us consider a sampling period of 1 second (\(T = 1s\)). During this period, the signal is sampled 8 times (\(N = 8\)).
What periodic frequencies can be properly sampled within this period?
Sampling Interval and Sampling Frequency
The sampling interval \(t_s\), which is the time between consecutive samples, is calculated as:
\[ t_s = \frac{T}{N} = \frac{1}{8} = 125 \text{ms} \]The corresponding sampling frequency \(f_s\), representing the number of samples per second, is:
\[ f_s = \frac{1}{t_s} = \frac{1}{0.125} = 8 \text{Hz} \]Possible Periodic Frequencies
Periodic frequencies that can be correctly sampled are those whose periods are exact multiples of the sampling interval. The lowest periodic frequency that fits within the 1-second sampling window is 1Hz (\(T = 8 t_s = 1 \text{s}\)). A frequency lower than this, such as 0.5 Hz (\(T = 2 \text{ s}\)), would not complete a full cycle within the sampling window, making it impossible to capture properly.
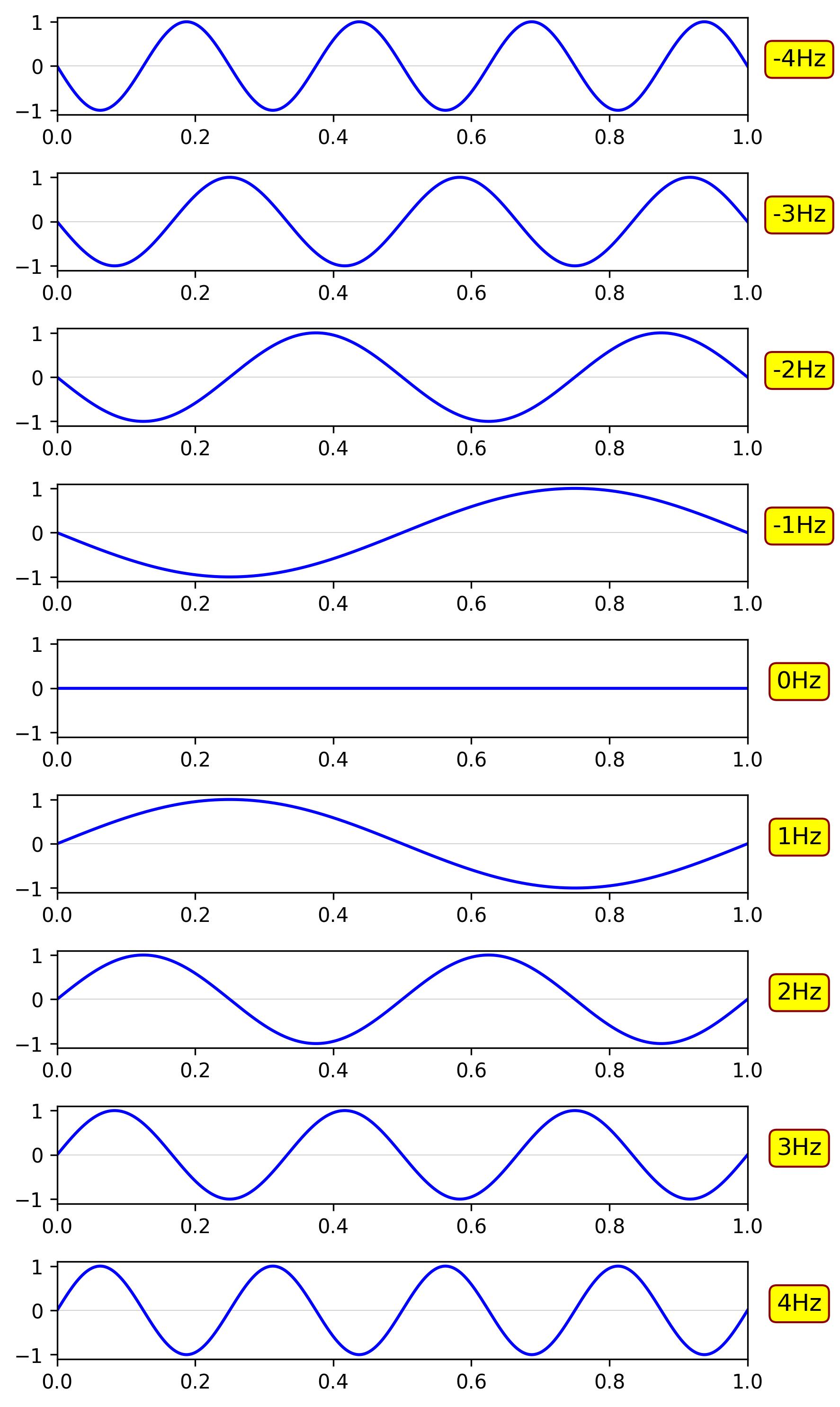
All integer multiples of 1Hz, such as 2Hz, 3Hz, 4Hz, and so on, will also fit the sampling window. Negative frequencies, such as -1Hz and its multiples, are also valid in this context.
Aliasing and Maximum Frequency
Due to the phenomenon of aliasing, the highest frequency that can be unambiguously sampled is determined by the Nyquist criterion, which states that the maximum non-ambiguous frequency is half of the sampling frequency:
\[ f_{\text{max}} = \frac{f_s}{2} = 4 \text{Hz} \]This means that the possible frequencies that can be accurately sampled range from 0Hz (DC or constant signal) to 4Hz for positive frequencies and from -4Hz to 0Hz for negative frequencies.
Possible Positive Frequencies:
- 0Hz (DC component)
- 1Hz
- 2Hz
- 3Hz
- 4Hz (Nyquist frequency)
Possible Negative Frequencies:
- -1Hz
- -2Hz
- -3Hz
- -4Hz (negative Nyquist frequency)
The following figure shows all the periodic frequencies that can be properly sampled at a sampling frequency of 8Hz, matching a 1-second sampling period.
Let us determine the periodic frequencies that correspond to a given sampling period \( T \).
The ratio between the sampling period \( T \) and the duration of one cycle of a sinusoid \( T_k \) should be an integer:
\[ \frac{T}{T_k} = k \]
where \( k \) is an integer.
The sampling period \( T \) can also be expressed as the product of the number of samples \( N \) and the sampling interval \( t_s \):
\[ T = N t_s \]
Substituting into the equation, we get:
\[ \frac{N t_s}{T_k} = k \]
The frequency of the sinusoid is then given by:
\[ f_k = \frac{1}{T_k} = \frac{k}{N t_s} = \frac{k}{N} f_s \]
where \( f_s = \dfrac{1}{t_s} \) is the sampling frequency.
The sinusoid with a periodic frequency that matches the sampling period \( T \) can be described as:
\[ x_k = \sin(2\pi f_k t) = \sin\left(2\pi \frac{k}{N} f_s t\right) \]
In the discrete domain, where \( t = n t_s \):
\[ x_k = \sin\left(2\pi \frac{k}{N} f_s n t_s\right) = \sin\left(2\pi \frac{k}{N} n\right) \]
This shows that we can describe the sinusoid purely in terms of discrete integers \( k \), \( N \), and \( n \) without reference to continuous time or frequency!
The maximum frequency should not exceed half the sampling frequency, as per the Nyquist-Shannon theorem:
\[ f_{k_{\text{max}}} < \frac{f_s}{2} = \frac{k_{\text{max}}}{N} f_s \]
Solving for \( k_{\text{max}} \):
\[ k_{\text{max}} = \frac{N f_s}{2 f_s} = \frac{N}{2} \]
For negative frequencies:
\[ k_{\text{min}} = -\frac{N}{2} \]
To summarize, the sinusoid with a periodic frequency that matches the sampling period \( T \) is given by:
\[ x_k = \sin\left(2\pi \frac{k}{N} n\right) \]
Where \( k \) is an integer in the range:
\[ -\frac{N}{2} \leq k \leq \frac{N}{2} \]
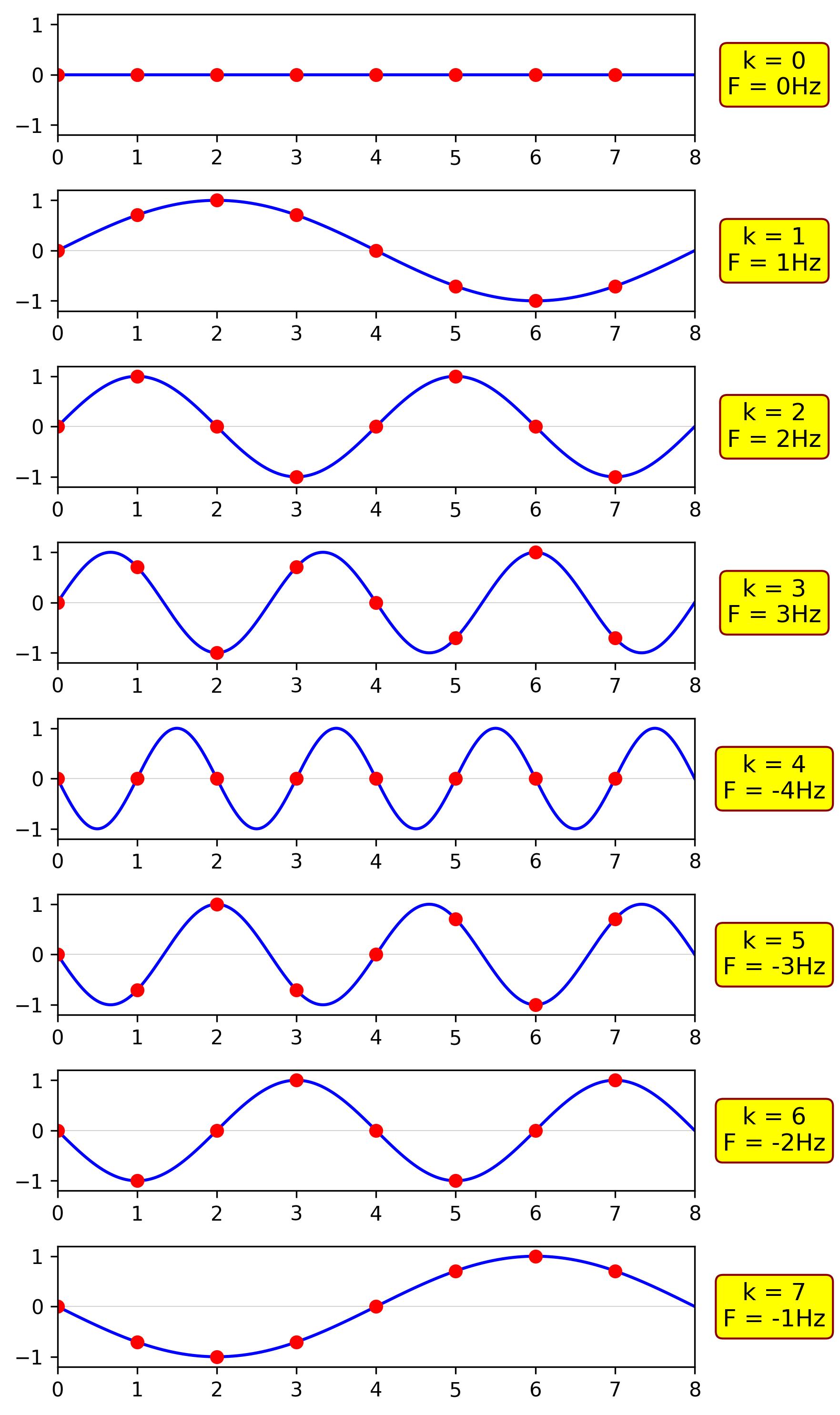
In our example where \( N = 8 \), the possible values of \( k \) are:
-4, -3, -2, -1, 0, 1, 2, 3, 4
In the clock hand sampling example, we showed that a frequency of the form \( f_0 + m f_s \) (where \( m \) is an integer) will alias with the frequency \( f_0 \). Therefore, the first aliasing frequency occurs at:
\[ f_{\text{alias}} = \frac{k}{N} f_s + 1 \cdot f_s = \frac{k + N}{N} f_s \]
Noticing that:
\[ -\frac{N}{2} + N = \frac{N}{2} \]
indicates that the index \( k = \frac{N}{2} \) is redundant, leading to the updated range for \( k \):
\[ -\frac{N}{2} \leq k < \frac{N}{2} \]
The possible values of \( k \) become:
-4, -3, -2, -1, 0, 1, 2, 3
To maintain non-negative \( k \) values, we can add \( N \) to negative \( k \) values, resulting in an equivalent signal. The following table illustrates the relationship between the original \( k \), the equivalent \( k \), and the corresponding frequencies in our example:
| Original \( k \) | Equivalent \( k \) | Frequency \( f_k \) |
|---|---|---|
| -4 | 4 | \( \frac{4}{8} f_s = 0.5f_s \) |
| -3 | 5 | \( \frac{5}{8} f_s \) |
| -2 | 6 | \( \frac{6}{8} f_s \) |
| -1 | 7 | \( \frac{7}{8} f_s \) |
| 0 | 0 | 0 |
| 1 | 1 | \( \frac{1}{8} f_s \) |
| 2 | 2 | \( \frac{2}{8} f_s \) |
| 3 | 3 | \( \frac{3}{8} f_s \) |
In Digital Signal Processing (DSP), the discrete frequency is described by a non-negative index \( k \), with the following interpretations:
- \(k = 0\) corresponds to zero frequency.
- \(0 < k \leq \frac{N}{2} - 1\) corresponds to positive frequencies.
- \(\frac{N}{2} \leq k \leq N - 1\) corresponds to negative frequencies.
So, the definition can be rewritten: A periodic frequency that matches a sampling period \( T \) and the number of samples \( N \) is given by:
\[ f_k = \frac{k}{N} f_s \]
Where:
\[ 0 \leq k \leq N - 1 \]
The periodic sinusoid with frequency \( f_k \) can be described as:
\[ x_k = \sin\left(2\pi \frac{k}{N} n\right) \]
The relation between the discrete frequencies and corresponding analog frequencies is:
\[ f = \begin{cases} \dfrac{k}{N} f_s, & 0 \leq k \leq \dfrac{N}{2} - 1 \\ \\ \dfrac{k - N}{N} f_s, & \dfrac{N}{2} \leq k \leq N - 1 \end{cases} \]
The following figures represent sampled sinusoids versus continuous sinusoids for various \( k \) values in our example.
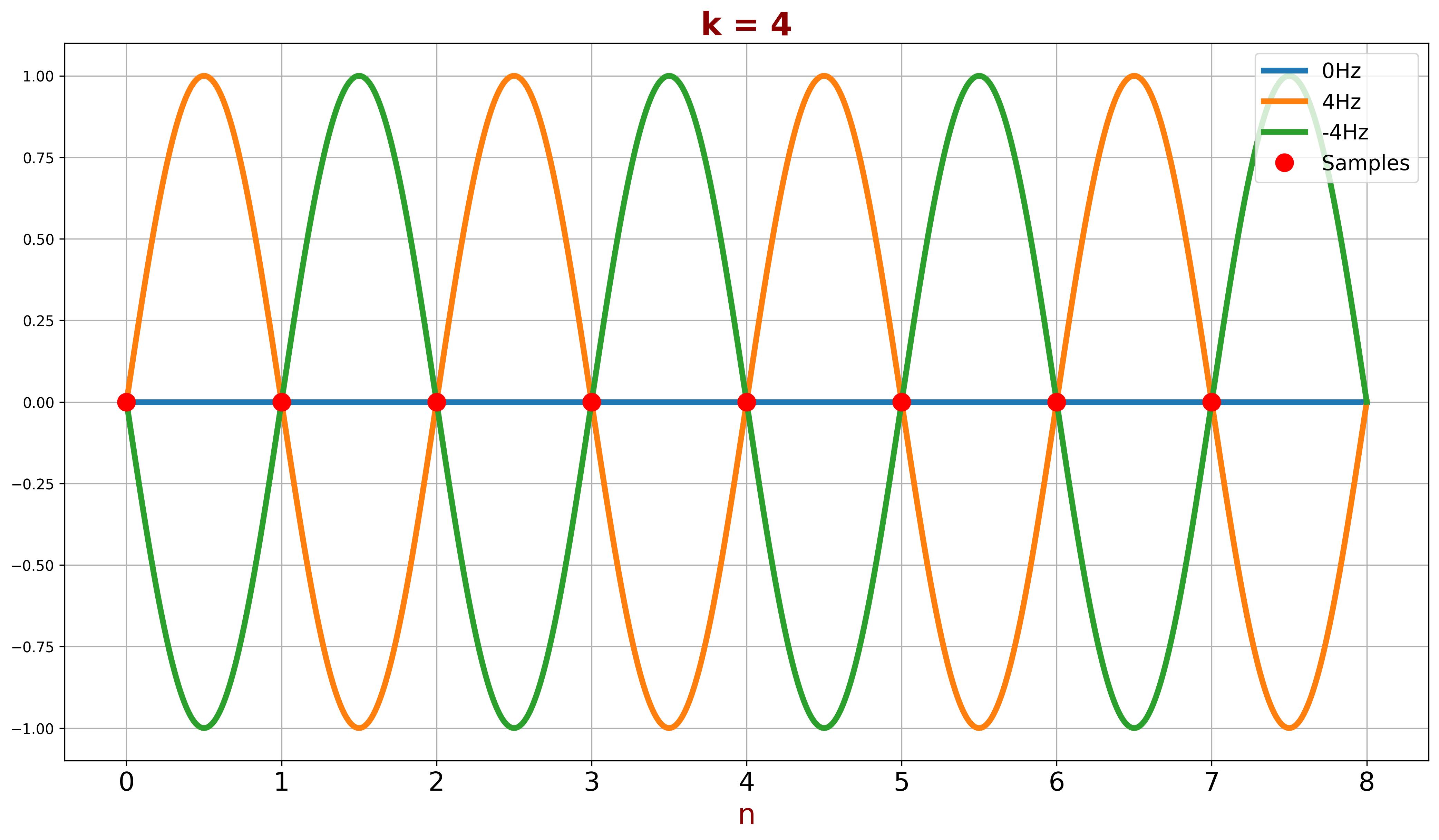
A special case is when \( k = 4 \). The following figure shows that the samples can match sinusoids at 0Hz, -4Hz, and 4Hz. As mentioned earlier, sampling at the Nyquist frequency (\( f_s = \frac{f_0}{2} \)) is not always sufficient, which is why the Nyquist-Shannon theorem defines \( f_s > \frac{f_0}{2} \).
Non-integer periods#
In our example, we used sinusoids with periods \( T \) that are exact multiples of the sampling interval. However, sinusoids can also have periods that are not integer multiples of the sampling interval.
For instance, consider a sinusoid with a frequency of 1.5Hz, which has a period of approximately 0.6667 seconds sampled with an interval \( t_s = 0.125ms \). The values of the sampled signal do not repeat at consistent intervals. This means that the periodic signal in the continuous domain does not maintain that periodicity when represented as discrete samples.
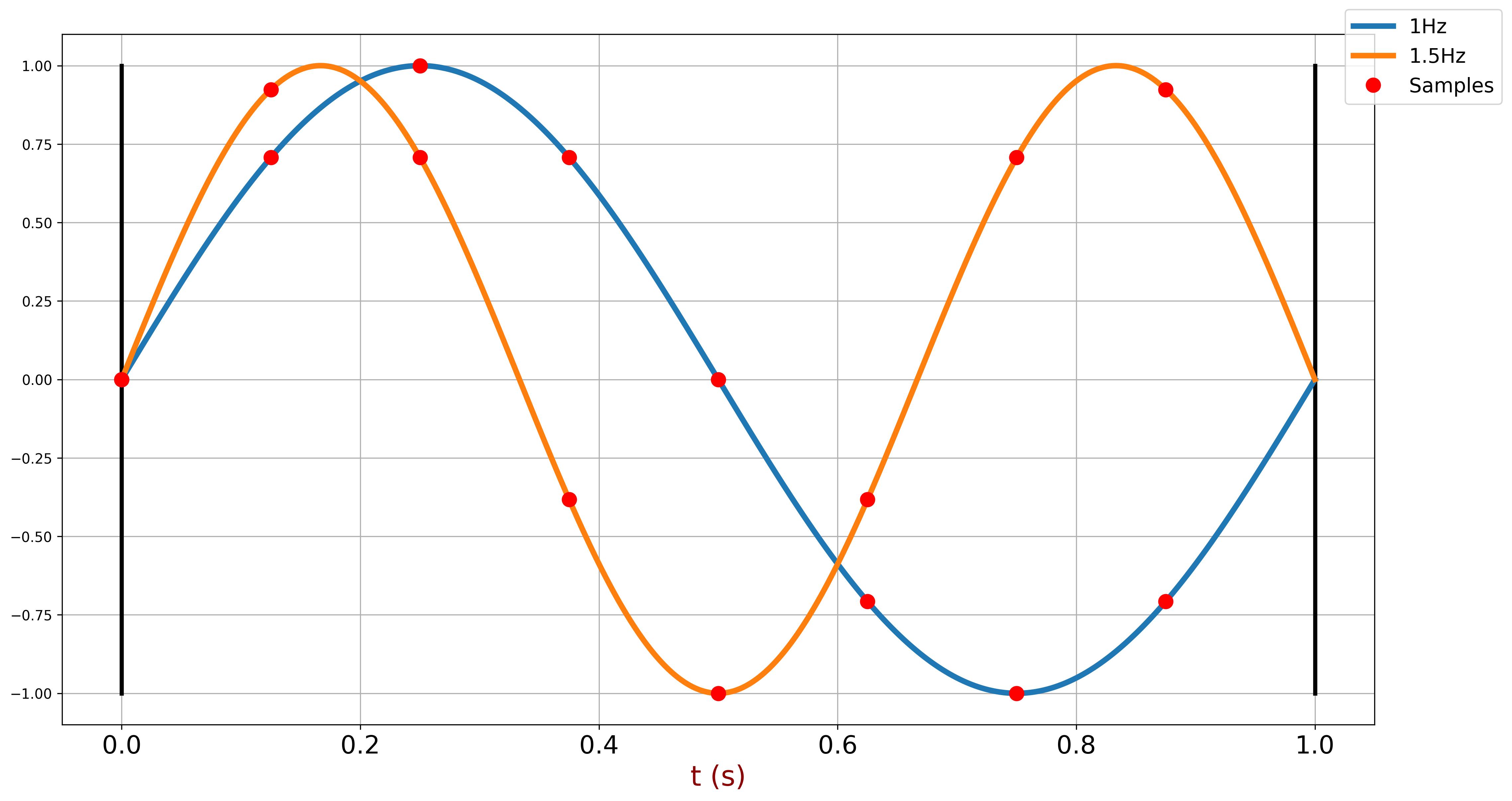
This lack of periodicity in the discrete domain occurs because the sampling interval doesn't align with the signal's period. As a result, the samples do not capture the full cycle of the signal in a way that would allow for repetition over successive sampling periods.
To properly sample both a 1Hz signal and a 1.5Hz signal, the sampling period should be chosen so that it can capture the periodic behavior of both signals. This requires selecting a sampling frequency that is a multiple of both signal frequencies, allowing the sampled values to accurately reflect the periodic nature of each signal.
For instance, to sample both a 1Hz and a 1.5Hz signal, you could use a sampling frequency that is a common multiple of the two, such as 3Hz. This would give a sampling period of \( \frac{1}{6} \) seconds, ensuring that both signals are properly sampled and their periodicity is preserved in the discrete domain.
The following figures represent sampled sinusoids versus continuous sinusoids for various \( k \) values in our example.