Essential Background
Before diving into Fourier Transform theory, I will first introduce some fundamental concepts, including radians, angular frequency, sinusoids, and negative frequency. If you're already familiar with these topics, feel free to skip this section and move on to the next.
Understanding Radians: A Natural Unit for Angles#
We’ve all been familiar with degrees as a unit of angle measurement since elementary school. A right angle is defined as 90 degrees, and a full circle is 360 degrees - a particularly convenient choice. The number 360 has many divisors (2, 3, 4, 5, 6, 8, 9, 10, 12, etc.), making it easy to divide angles without needing fractions. This allows for natural subdivisions, such as:
4 quadrants (90° each)
6 equilateral triangle segments (60° each)
12 parts (30° each, like a clock)
The origin of 360 degrees traces back to the Babylonians, who used a base-60 (sexagesimal) number system around 3000 BCE. They approximated a year as 360 days, based on lunar cycles, which reinforced their system for measuring circles.
While degrees are an arbitrary unit of angle measurement, radians naturally correspond to arc length on a unit circle (a circle with a radius of 1). An angle of one radian, measured from the center, subtends an arc with a length of 1.
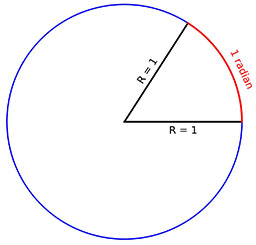
A full circle is \( 2\pi \) radians, corresponding to the unit circle's circumference (\( P = 2\pi R = 2\pi \) when \( R = 1 \)). Since \( 2\pi \) is irrational, expressing natural fractions of \( 2\pi \) in decimal form can be cumbersome. For example, a right angle (90°) is approximately 1.5708 radians, and a 30° angle is about 0.5236 radians.
To simplify notation, it is more convenient to express angles as fractions of \( \pi \). For instance:
A right angle (90°) is \( \pi /2 \) radians
A 30° angle is \( \pi /6 \) radians
This approach avoids long decimal representations, making trigonometry and calculus calculations more intuitive.
Radians simplify mathematical formulas because they directly relate angles to arc length. In calculus, trigonometry, and physics, they eliminate conversion factors, making equations cleaner and more intuitive.
In this text, angles are measured in radians unless otherwise specified.
Sinusoids: The Foundation of Signals#
Sinusoids are the foundation of waves, oscillations, and signal processing. Sinusoidal functions appear everywhere in science and engineering, whether describing sound, light, electrical signals, or even quantum mechanics. They provide a natural way to represent periodic motion, such as rotating objects, vibrating strings, and alternating currents.
More importantly, sinusoids serve as the building blocks of complex signals. Through Fourier analysis, any periodic signal, no matter how intricate, can be decomposed into a sum of simple sine waves. This makes them indispensable in communication systems, control theory, and digital signal processing.
In this chapter, we will explore the mathematical properties of sinusoids, their connection to rotation, and how they form the basis for understanding signals and wave phenomena.
Angular Frequency and Frequency
For example, let’s consider a single-handed clock, where the clock hand rotates counterclockwise. When the hand points to 3 o’clock, the angle between the \( x \)-axis and the clock hand is zero. As time progresses, the clock hand continues rotating, and after a time interval \( \Delta t \), it sweeps an angle \( \Delta \phi \).
In the context of oscillations and waves, angles are referred to as "phase" because they represent a position within a cycle of periodic motion.
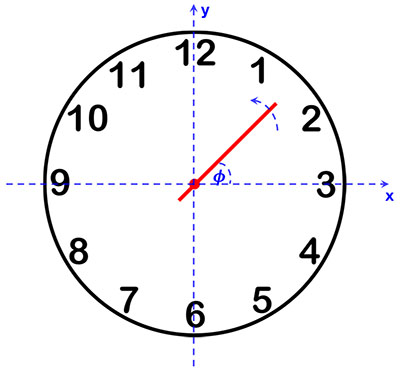
The angular frequency \( \omega \) is the rate of change of phase with respect to time and is given by:
\[ \omega = \frac{\Delta \phi}{\Delta t} \]
or, in differential form:
\[ \omega = \frac{d\phi}{dt} \]
The unit of angular frequency is radians per second (rad/s).
The time \( T \) required for the clock hand to complete one full revolution is called the period. The frequency \( f \) is the number of cycles per second and is given by:
\[ f = \frac{1}{T} \]
The unit of frequency is Hertz (Hz).
Since one full cycle corresponds to an angle of \( 2\pi \) radians, the relationship between frequency \( f \) and angular frequency \( \omega \) is:
\[ \omega = 2\pi f \]
Sinusoidal Projections
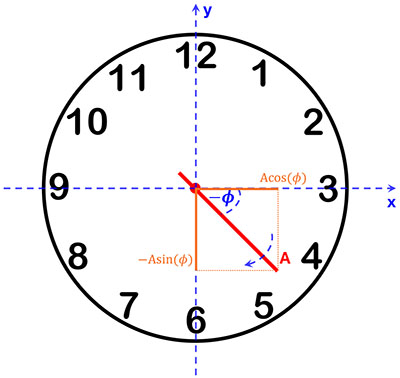
Let’s examine the projections of the clock hand onto the \(x\) and \(y\) axes. At a given moment \( t \), the phase (angle) between the clock hand and the \( x \)-axis is \( \phi \). If the clock hand has a length \( A \), its projections onto the axes are:
\( x \)-axis projection: \( A\cos(\phi) \)
\( y \)-axis projection: \( A\sin(\phi) \)
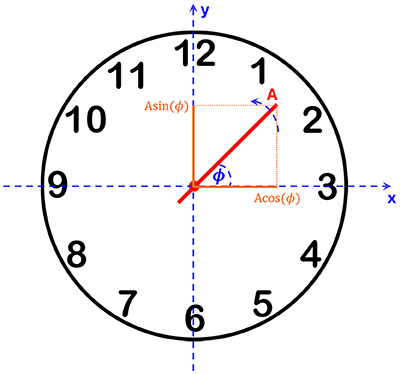
When the clock hand rotates with an angular velocity \( \omega \), the phase \( \phi \) at time \( t \) is:
\[ \phi(t) = \omega t \]
If the initial angle at \( t = 0 \) is \( \phi(0) = 0 \), the projections of the clock hand at time \( t \) are:
\( x \)-axis projection:
\[ A\cos(\omega t) = A\cos(2\pi f t) \]
\( y \)-axis projection:
\[ A\sin(\omega t) = A\sin(2\pi f t) \]
The following plot shows the \(x\)-axis and \(y\)-axis projections as a function of time:
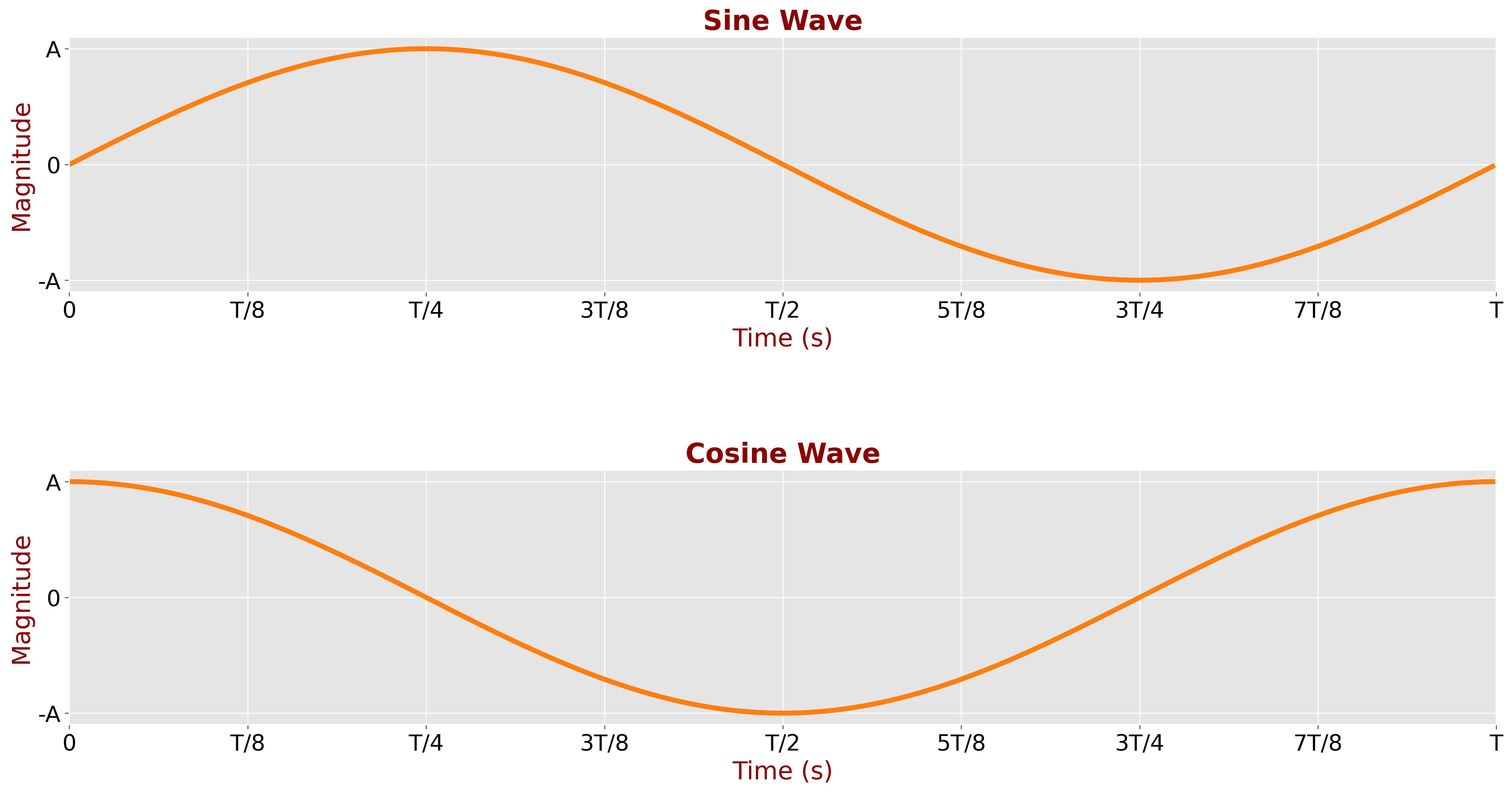
Similarly, we can plot the \(x\)-axis and \(y\)-axis projections as a function of phase:
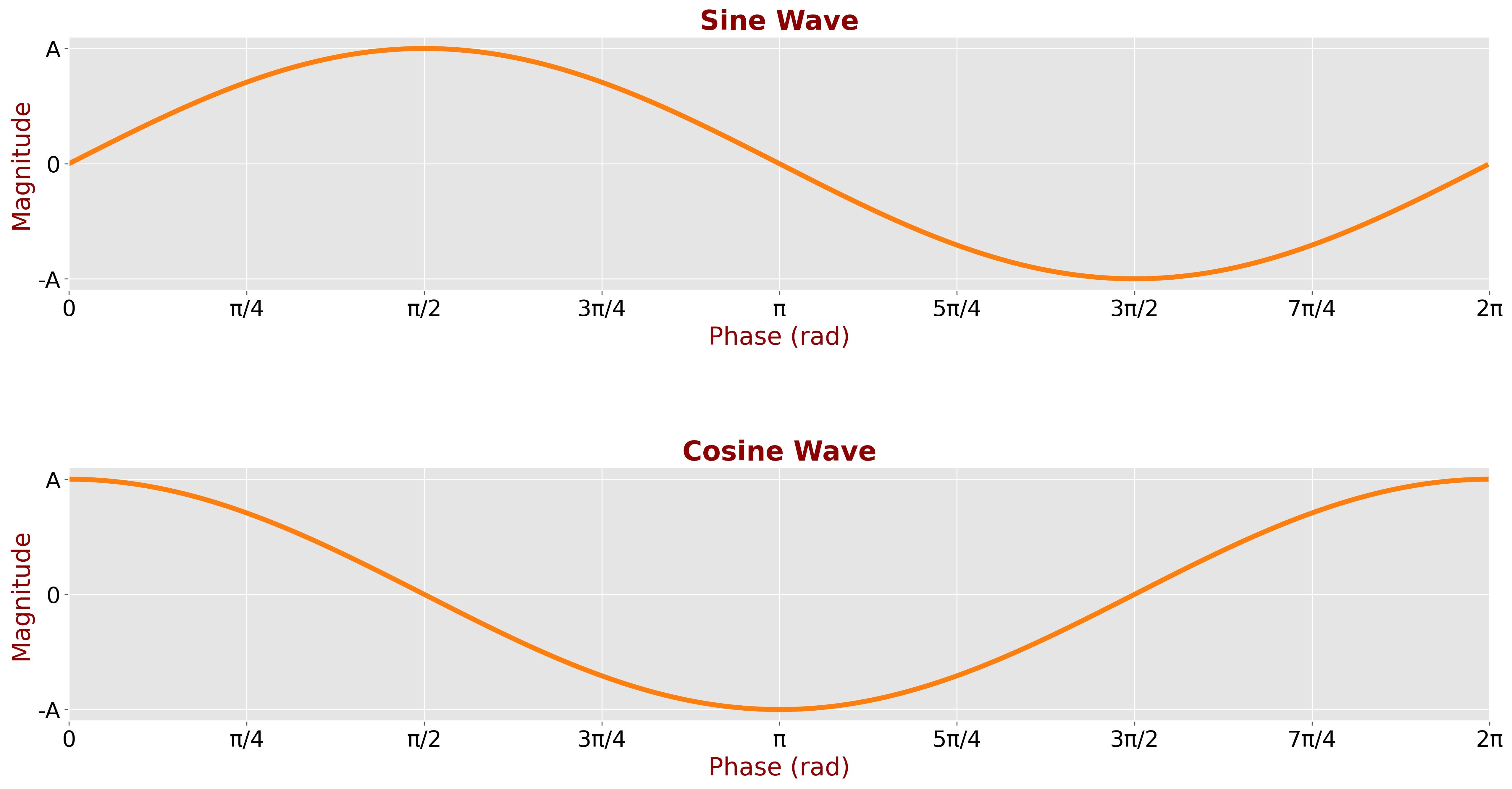
The two plots appear similar since the relationship between phase and time is constant and equals \( \omega \) :
\[ \frac{\phi(t)}{t} = \omega \]
If the clock hand starts at an initial phase \( \phi_{t=0} = \varphi \), the projections at time \( t \) are:
\( x \)-axis projection:
\[ A\cos(\omega t + \varphi) = A\cos(2\pi f t + \varphi) \]
\( y \)-axis projection:
\[ A\sin(\omega t + \varphi) = A\sin(2\pi f t + \varphi) \]
Many signals in nature and engineering can be described using sine and cosine functions because they naturally represent periodic and oscillatory behavior, modeling how signals evolve over time.
Negative Frequency#
The English language has distinct terms for two closely related concepts: speed and velocity. When a driver looks at a car’s speedometer, it displays the car’s speed - a measure of how fast the vehicle is moving, without indicating direction. However, an outside observer can measure the car's velocity, which includes both speed and direction. If we define movement toward the east as positive, then a car moving east has a positive velocity, while a car going west has a negative velocity.
Many other languages do not make this distinction.
Unlike speed and velocity, the term frequency lacks a similar distinction in everyday language. Let’s revisit our clock analogy. If the clock hand moves counterclockwise, the angle (phase) between the \( x \)-axis and the hand increases in the positive direction. The rate of this change, known as the angular frequency \( \omega \), is positive.
Conversely, if the clock hand moves clockwise, the angle decreases in the negative direction, meaning the angular frequency \( \omega \) is negative.
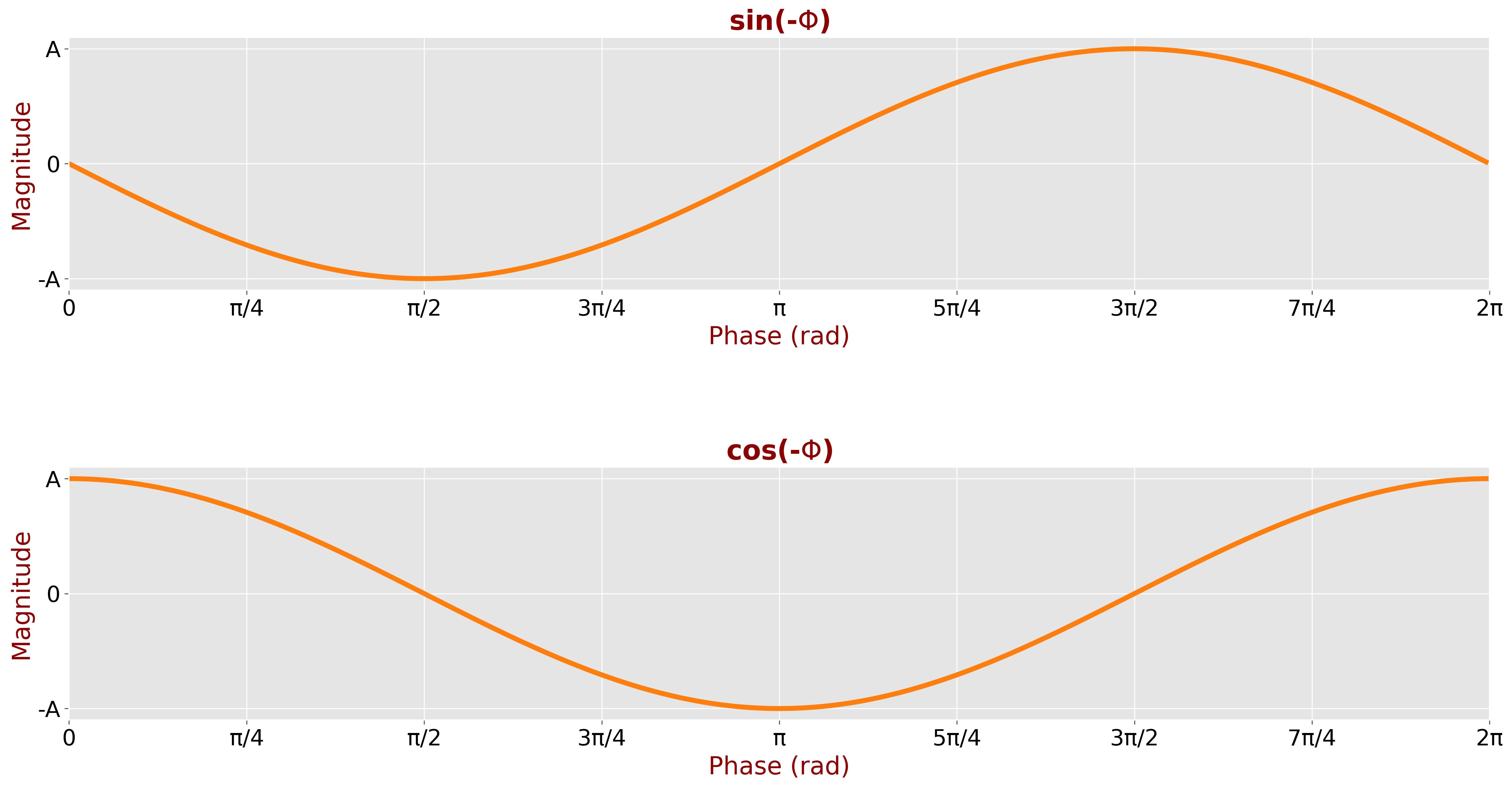
You can see the effect of negative frequency by examining sine and cosine projections:
The sine projection for a negative frequency is the opposite of the sine projection for a positive frequency. This follows from the fact that sine is an odd function:
\[ \sin(\phi) = -\sin(-\phi) \]
The cosine projection, however, remains unchanged because cosine is an even function:
\[ \cos(\phi) = \cos(-\phi) \]
If there is a difference between positive and negative frequencies, why does a spectrum analyzer display only positive frequencies?
Note
A spectrum analyzer is a test instrument that displays the power spectrum of an input signal, showing the distribution of frequency magnitudes.
This occurs because the power of both positive and negative frequencies is computed as:
\[ P = |\sin(\phi)|^2 \]
Since squaring removes the sign, the spectrum analyzer cannot distinguish between positive and negative frequencies and displays positive and negative frequencies together.
On the other hand, signal analyzers that measure both the magnitude and phase of a signal’s frequency components can distinguish between positive and negative frequencies. These analyzers process complex signals (I/Q data), which preserve directional information, allowing them to differentiate between the two.