Fourier Convergence Theorem#

We have seen that any periodic signal composed of sinusoidal functions can be decomposed into frequency components using the Fourier Series. But what about other periodic waveforms, such as square waves or triangular waves?

Definition#

Fourier's Theorem states:

Fourier's Theorem Definition

Any function defined on the interval \([-T,T]\) can be expressed as a sum of an infinite number of pure sine and cosine waves - Fourier Series.
The frequencies of these sinusoidal components are integer multiples (harmonics) of the signal's fundamental frequency.

The Fourier Series representation of a periodic function \( x(t) \) is given by:

                                                    \[
                                                    x(t) = a_0 + \sum\limits_{n=1}^{\infty} \left( b_n \sin(n\omega_1 t) + a_n \cos(n\omega_1 t) \right)
                                                    \]
                                                

Where:

\(\omega_1 = \frac{2\pi}{T}\): The fundamental angular frequency, derived from the signal's period \( T \).
\(n\): The harmonic number (integer multiples of the fundamental frequency).
\(a_0\): The average (DC) component of the signal.
\(a_n, b_n\): The Fourier coefficients, representing the amplitudes of the cosine and sine components.

The Fourier Series converges if the function is piecewise smooth.
At jump discontinuities of the periodic extension, the Fourier Series converges to:

\[ \frac{1}{2} \left( \bar{x}(t^-) + \bar{x}(t^+) \right) \]

The Fourier Convergence Theorem might seem unclear. What exactly does it mean for a function to be piecewise smooth? What is convergence? How do jump discontinuities affect the result? What are the jump discontinuities? And what is the periodic extension?

We will revisit the definition, but first, let’s go through two examples to develop intuition.

Important note!

As mentioned at the beginning of this chapter, the Fourier Series serves as a tool for theoretical spectral analysis of continuous periodic signals. However, its implementation involves mathematical derivations and the calculation of integrals.

The goal of this text is to offer a practical perspective on Fourier Analysis, focusing on intuitive understanding rather than delving into rigorous mathematical theory.

That said, some readers may feel comfortable exploring math. The remainder of this chapter provides a deeper explanation of the Fourier Theorem, along with several examples that illustrate its applications. If you find this section challenging, feel free to skip it without affecting your understanding of the subsequent chapters.

Examples#

Square wave

Let us begin with the square wave as an example. Consider the following odd periodic square wave function:

\[ x(t) = \begin{cases} 1, & 0 \leq x < \frac{T}{2} \\ -1, & \frac{T}{2} \leq x < T \end{cases} \]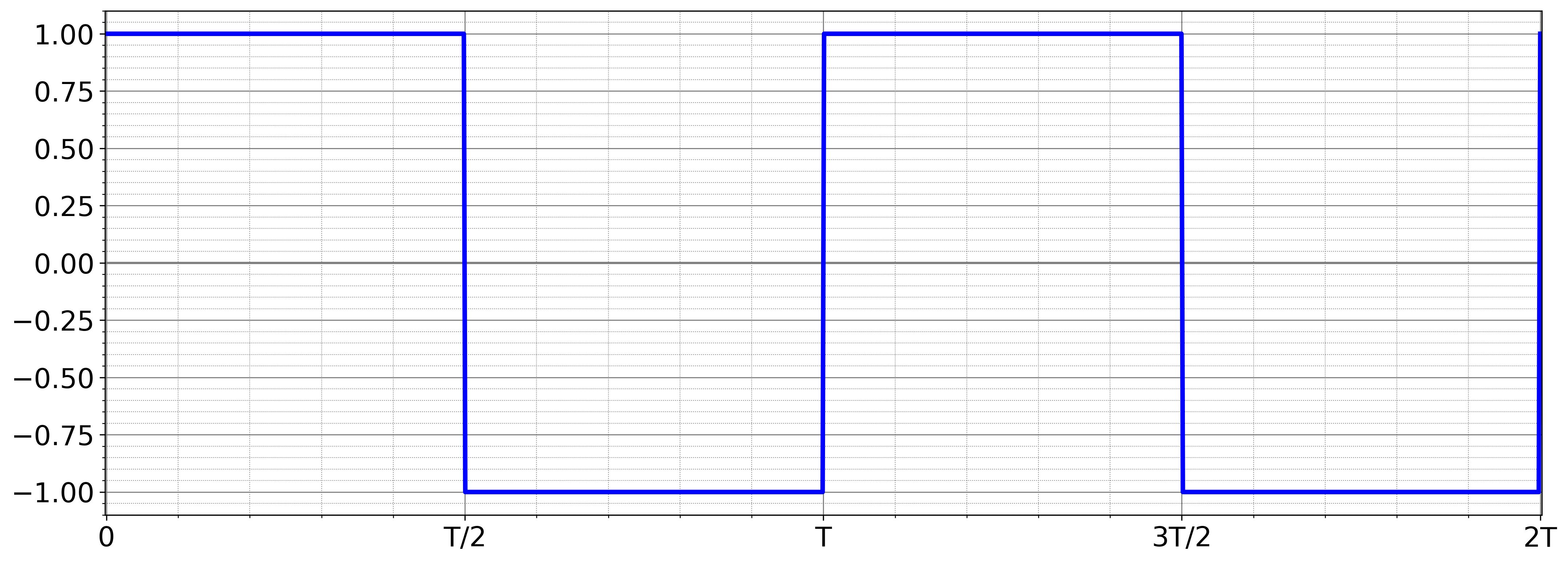

Finding coefficient \( a_0 \):

\[ a_0 = \frac{1}{T} \int\limits_0^T x(t) dt = \color{green}{\frac{1}{T} \int\limits_0^{T/2} x(t) dt} \color{#222832}{\ +\ } \color{red}{\frac{1}{T} \int\limits_{T/2}^{T} x(t) dt} \]

Expanding and solving:

\[ a_0 = \color{green}{\frac{1}{T} \int\limits_0^{T/2} 1 \, dt} \color{#222832}{\ +\ } \color{red}{\frac{1}{T} \int\limits_{T/2}^{T} (-1) \, dt} \] \[ = \color{green}{\frac{1}{T} \left[ t \right]_0^{T/2}} \color{#222832}{\ -\ } \color{red}{\frac{1}{T} \left[ t \right]_{T/2}^{T}} \] \[ = \color{green}{\frac{T}{2T}}\color{#222832} {\ -\ } \color{red}{\frac{T - T/2}{T}} \color{#222832}{\ = 0} \]

Finding coefficients \( a_m \):

\[ a_m = \frac{2}{T} \int\limits_0^T x(t) \cos\left(\frac{2\pi m}{T} t\right) dt \]

Breaking the integral into segments:

\[ a_m = \color{green}{\frac{2}{T} \int\limits_0^{T/2} \cos\left(\frac{2\pi m}{T} t\right) dt} \color{#222832}{\ +\ } \color{red}{\frac{2}{T} \int\limits_{T/2}^{T} (-1) \cos\left(\frac{2\pi m}{T} t\right) dt} \]

Performing integration:

\[ a_m = \color{green}{\frac{2}{T} \left[ \frac{1}{\frac{2\pi m}{T}} \sin\left(\frac{2\pi m}{T} t\right) \right]_0^{T/2}} \color{#222832}{\ -\ } \color{red}{\frac{2}{T} \left[ \frac{1}{\frac{2\pi m}{T}} \sin\left(\frac{2\pi m}{T} t\right) \right]_{T/2}^{T}} \] \[ = \color{green}{\frac{1}{\pi m} \left( \sin\left(\frac{2\pi m}{T} \cdot \frac{T}{2}\right) - \sin(0) \right)} \color{#222832}{\ -\ } \color{red}{\frac{1}{\pi m} \left( \sin\left(\frac{2\pi m}{T} \cdot T\right) - \sin\left(\frac{2\pi m}{T} \cdot \frac{T}{2}\right) \right)} \] \[ = \color{green}{\frac{1}{\pi m} \sin(\pi m)} \color{#222832}{\ -\ } \color{red}{\frac{1}{\pi m} \left( \sin(2\pi m) - \sin(\pi m) \right)} \color{#222832}{\ = 0} \]

All cosine coefficients \( a_m \) equal zero.

Finding coefficients \( b_m \):

\[ b_m = \frac{2}{T} \int\limits_0^T x(t) \sin\left(\frac{2\pi m}{T} t\right) dt \]

Breaking the integral into segments:

\[ b_m = -\color{green}{\frac{2}{T} \left[ \frac{1}{\frac{2\pi m}{T}} \cos\left(\frac{2\pi m}{T} t\right) \right]_0^{T/2}} \color{#222832}{\ +\ } \color{red}{\frac{2}{T} \left[ \frac{1}{\frac{2\pi m}{T}} \cos\left(\frac{2\pi m}{T} t\right) \right]_{T/2}^{T}} \] \[ = -\color{green}{\frac{1}{\pi m} \left( \cos\left(\frac{2\pi m}{T} \cdot \frac{T}{2}\right) - \cos(0) \right)} \color{#222832}{\ +\ } \color{red}{\frac{1}{\pi m} \left( \cos\left(\frac{2\pi m}{T} \cdot T\right) - \cos\left(\frac{2\pi m}{T} \cdot \frac{T}{2}\right) \right)} \] \[ = -\color{green}{\frac{1}{\pi m} \left( \cos(\pi m) - 1 \right)} \color{#222832}{\ +\ } \color{red}{\frac{1}{\pi m} \left( \cos(2\pi m) - \cos(\pi m) \right)} \] \[ = -\color{green}{\frac{1}{\pi m} \left( \cos(\pi m) - 1 \right)} \color{#222832}{\ +\ } \color{red}{\frac{1}{\pi m} \left( 1 - \cos(\pi m) \right)} \] \[ = \frac{2}{\pi m} ( 1 - \cos(\pi m) ) \]

For even \( m \), \( \cos(\pi m) = 1 \), so \( b_m = 0 \).

For odd \( m \), \( \cos(\pi m) = -1 \), so: \( \dfrac{4}{\pi m} \)

                                                \[
                                                b_m =
                                                \begin{cases}
                                                \dfrac{4}{\pi m}, & \text{if } m = 2k - 1, \quad k \in \mathbb{N} \\
                                                0, & \text{otherwise}
                                                \end{cases}
                                                \]
                                            

Thus, the Fourier Series of the square wave is:

\[ x(t) = a_0 + \sum\limits_{m=1}^{\infty} \left( b_m \sin\left(\frac{2\pi m}{T} t\right) + a_m \cos\left(\frac{2\pi m}{T} t\right) \right) \] \[ = 0 + \sum\limits_{m=1}^{\infty} \left( b_m \sin\left(\frac{2\pi m}{T} t\right) + 0 \cdot \cos\left(\frac{2\pi m}{T} t\right) \right) \] \[ = \sum\limits_{m=1}^{\infty} b_m \sin\left(\frac{2\pi m}{T} t\right) \] \[ = \frac{4}{\pi} \sum\limits_{m=1,3,5,\dots}^{\infty} \frac{1}{m} \sin\left(\frac{2\pi m}{T} t\right) \]

\[ x(t) = \frac{4}{\pi} \left( \frac{\sin\left(\dfrac{2\pi \cdot 1}{T} t\right)}{1} + \frac{\sin\left(\dfrac{2\pi \cdot 3}{T} t\right)}{3} + \frac{\sin\left(\dfrac{2\pi \cdot 5}{T} t\right)}{5} + \dots \right) \]

Observations:

The square wave is composed of an infinite sum of sine waves with frequencies \( \dfrac{m}{T} \) and amplitudes that decay as \( \dfrac{1}{m} \).
Adding more harmonics improves the approximation of the square wave.

The following visualizations illustrate the effect of adding harmonics:

First two harmonics: Shows the initial approximation.
First three harmonics: Further improves the shape.
First four harmonics: Closer to the square wave.
100 harmonics: Closely resembles the square wave.

The following figures illustrate these approximations:

The first two harmonics and their sum.
The first three harmonics and their sum.
The first four harmonics and their sum.
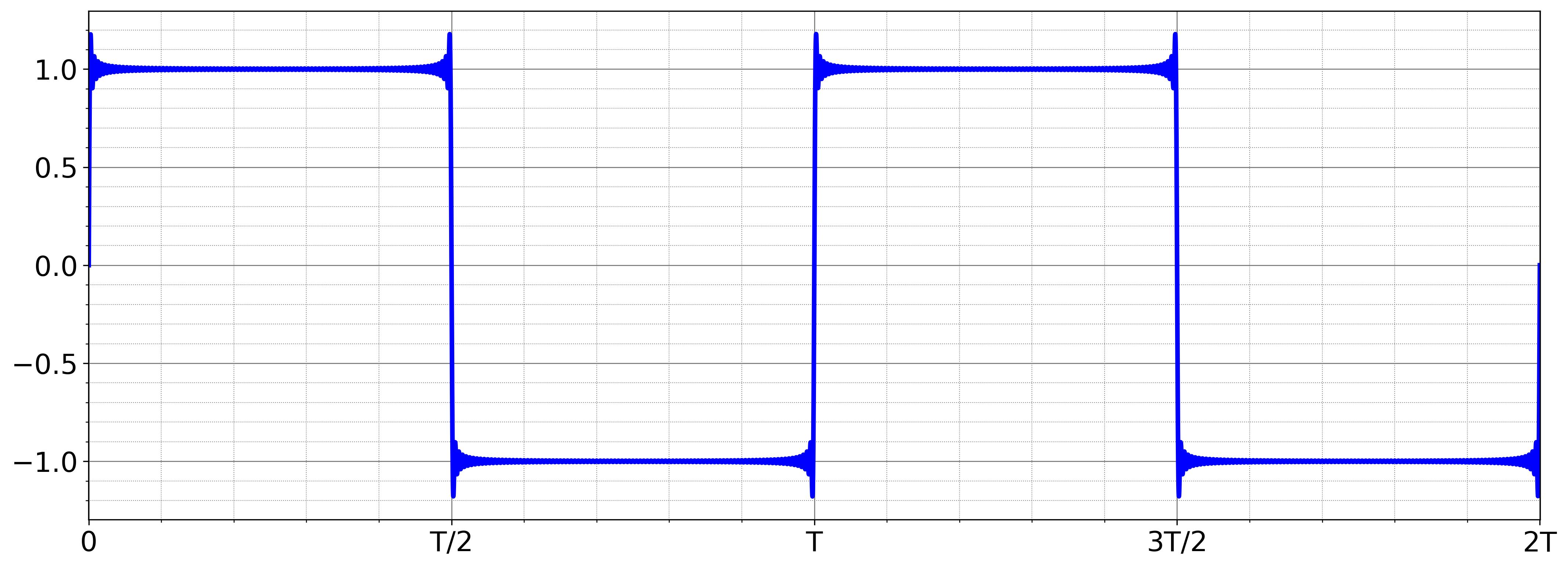
The sum of 100 harmonics, closely resembling the square wave.

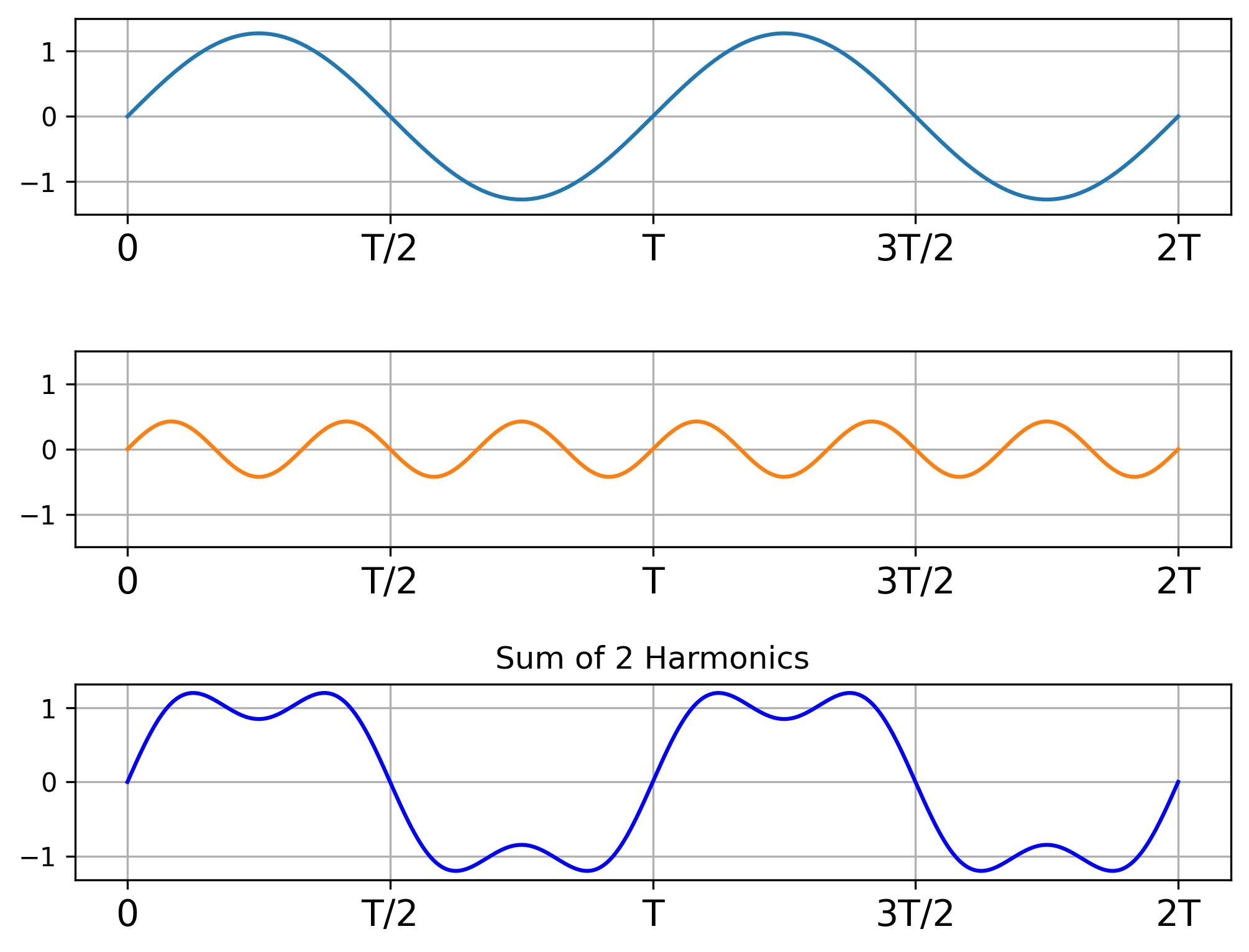
The following figure shows the first two harmonics and their sum:

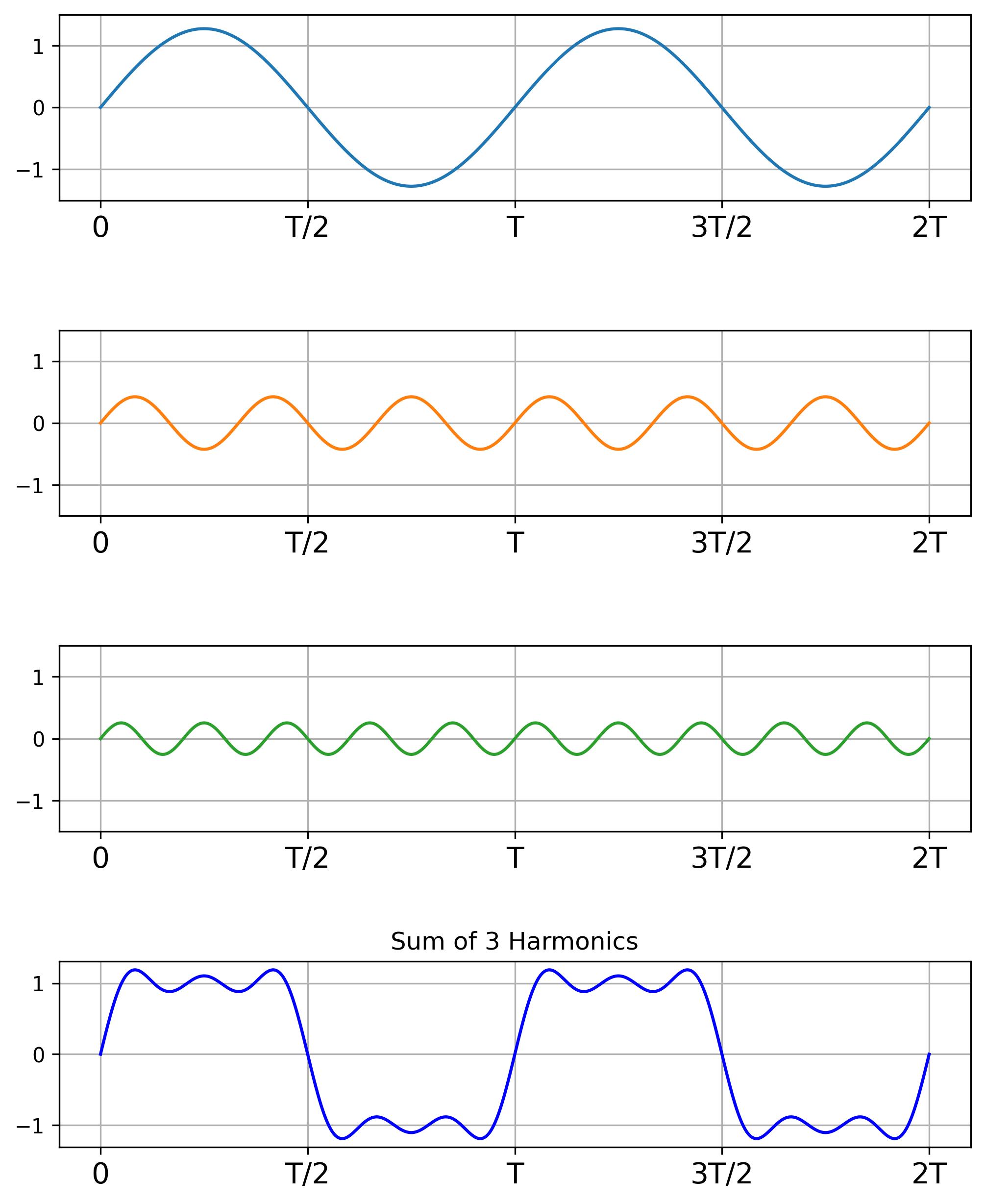
The following figure shows the first three harmonics and their sum:

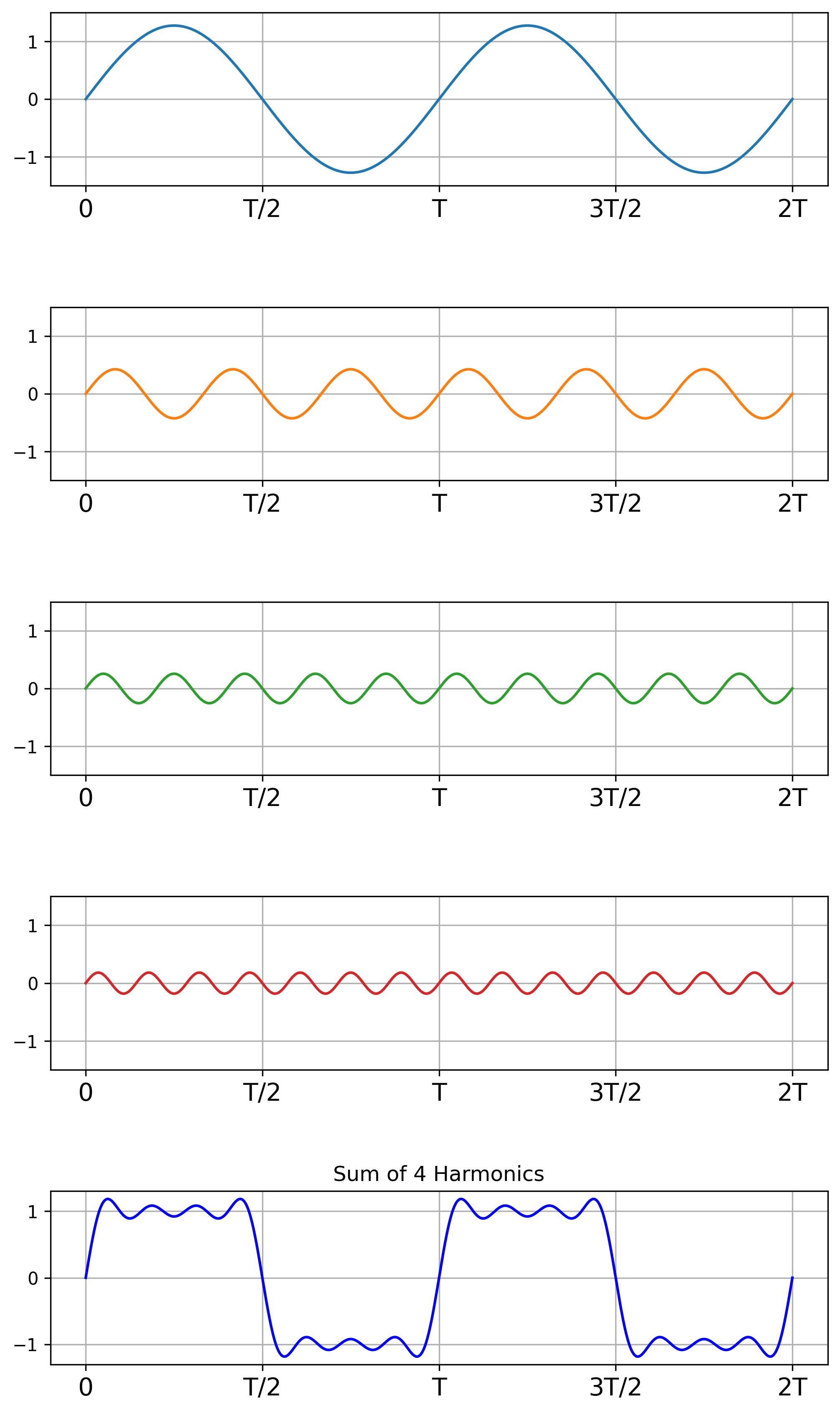
The following figure shows the first four harmonics and their sum:

As we add more harmonics, their sum resembles the square wave more. The following figure describes the sum of 100 harmonics.

Triangle wave

Now, consider an even periodic triangle wave function:

\[ x(t) = \begin{cases} -\dfrac{2A}{T} t, & -\dfrac{T}{2} \leq x < 0 \\ \\ \dfrac{2A}{T} t, & 0 \leq x < \dfrac{T}{2} \end{cases} \]

Finding coefficients \( a_0 \):

\[ a_0 = \frac{1}{T} \int\limits_{-T/2}^{T/2} x(t) dt \]

Breaking the integral into segments:

\[ a_0 = \color{green}{\frac{1}{T} \int\limits_{-T/2}^{0} x(t) dt} \color{#222832}{\ +\ } \color{red}{\frac{1}{T} \int\limits_{0}^{T/2} x(t) dt} \] \[ = \color{green}{\frac{1}{T} \int\limits_{-T/2}^{0} \left(-\frac{2A}{T} t \right) dt} \color{#222832}{\ +\ } \color{red}{\frac{1}{T} \int\limits_{0}^{T/2} \left(\frac{2A}{T} t \right) dt} \] \[ a_0 = -\color{green}{\frac{2A}{T^2} \int\limits_{-T/2}^{0} t dt} \color{#222832}{\ +\ } \color{red}{\frac{2A}{T^2} \int\limits_{0}^{T/2} t dt} \]

Performing integration:

\[ a_0 = -\color{green}{\dfrac{2A}{T^2} \left[ \dfrac{t^2}{2} \right]_{-T/2}^{0}} \color{#222832}{\ +\ } \color{red}{\frac{2A}{T^2} \left[ \dfrac{t^2}{2} \right]_{0}^{T/2}} \] \[ a_0 = \color{green}{\dfrac{A}{4}} \color{#222832}{\ +\ } \color{red}{\dfrac{A}{4}} \]

                                                \[
                                                a_0 = \dfrac{A}{2}
                                                \]
                                            

Finding coefficients \( a_m \):

\[ a_m = \frac{2}{T} \int\limits_{-T/2}^{T/2} x(t) \cos\left( \frac{2\pi m}{T} t \right) dt \]

Breaking the integral into segments:

\[ a_m = \color{green}{\frac{2}{T} \int\limits_{-T/2}^{0} \left(-\frac{2A}{T} t\right) \cos\left( \frac{2\pi m}{T} t \right) dt} \color{#222832}{\ +\ } \color{red}{\frac{2}{T} \int\limits_{0}^{T/2} \left(\frac{2A}{T} t\right) \cos\left( \frac{2\pi m}{T} t \right) dt} \] \[ = \frac{4A}{T^2} \left(\color{red}{ \int\limits_{0}^{T/2} t \cos\left( \frac{2\pi m}{T} t \right) dt} \color{#222832}{\ -\ } \color{green}{\int\limits_{-T/2}^{0} t \cos\left( \frac{2\pi m}{T} t \right) dt} \color{#222832}{ }\right) \] \[ = \frac{2A}{(\pi m)^2} (\cos(\pi m) - 1) \]

You can find the integral solution in Appendix C.

For even \( m \), \( \cos(\pi m) = 1 \), therefore \( a_{m} = 0 \).

For odd \( m \), \( \cos(\pi m) = -1 \), therefore \( a_{m} = -\dfrac{4A}{(\pi m)^2} \).

                                                \[
                                                a_m =
                                                \begin{cases}
                                                -\dfrac{4A}{(\pi m)^2}, & \text{if } m=2k-1, k \in \mathbb{N} \\
                                                0, & \text{otherwise}
                                                \end{cases}
                                                \]
                                            

Finding coefficients \( b_m \):

\[ b_m = \frac{2}{T} \int\limits_{-T/2}^{T/2} x(t) \sin\left( \frac{2\pi m}{T} t \right) dt \]

Breaking the integral into segments:

\[ b_m = \color{green}{\frac{2}{T} \int\limits_{-T/2}^{0} \left(-\frac{2A}{T} t\right) \sin\left( \frac{2\pi m}{T} t \right) dt} \color{#222832}{\ +\ } \color{red}{\frac{2}{T} \int\limits_{0}^{T/2} \left(\frac{2A}{T} t\right) \sin\left( \frac{2\pi m}{T} t \right) dt} \] \[ = \frac{4A}{T^2} \left( \color{red}{\int\limits_{0}^{T/2} t \sin\left( \frac{2\pi m}{T} t \right) dt} \color{#222832}{\ -\ } \color{green}{\int\limits_{-T/2}^{0} t \sin\left( \frac{2\pi m}{T} t \right) dt} \color{#222832}{} \right) = 0 \]

You can find the integral solution in Appendix C.

Fourier Series of even Triangle Wave:

\[ x(t) = a_0 + \sum\limits_{m=1}^{\infty} \left( b_m \sin\left( \dfrac{2\pi m}{T} t \right) + a_m \cos\left( \dfrac{2\pi m}{T} t \right) \right) \] \[ = \dfrac{A}{2} + \sum\limits_{m=1}^{\infty} a_m \cos\left( \dfrac{2\pi m}{T} t \right) \] \[ = \dfrac{A}{2} - \dfrac{4A}{\pi^2} \sum\limits_{m=1,3,5,\dots}^{\infty} \dfrac{\cos\left( \dfrac{2\pi m}{T} t \right)}{m^2} \] \[ \] \[ x(t) = \dfrac{A}{2} - \dfrac{4A}{\pi^2} \left( \dfrac{\cos\left( \dfrac{2\pi}{T} t \right)}{1} + \dfrac{\cos\left( \dfrac{6\pi}{T} t \right)}{3^2} + \dfrac{\cos\left( \dfrac{10\pi}{T} t \right)}{5^2} + \dots \right) \]

Observations:

The triangle wave consists of an infinite sum of cosine waves with frequencies \( \dfrac{m}{T} \) and amplitudes decaying as \( \dfrac{1}{m^2} \).
Visualizations follow the same pattern as the square wave, where increasing harmonics result in better approximations.

The following figure shows the first two harmonics and their sum:

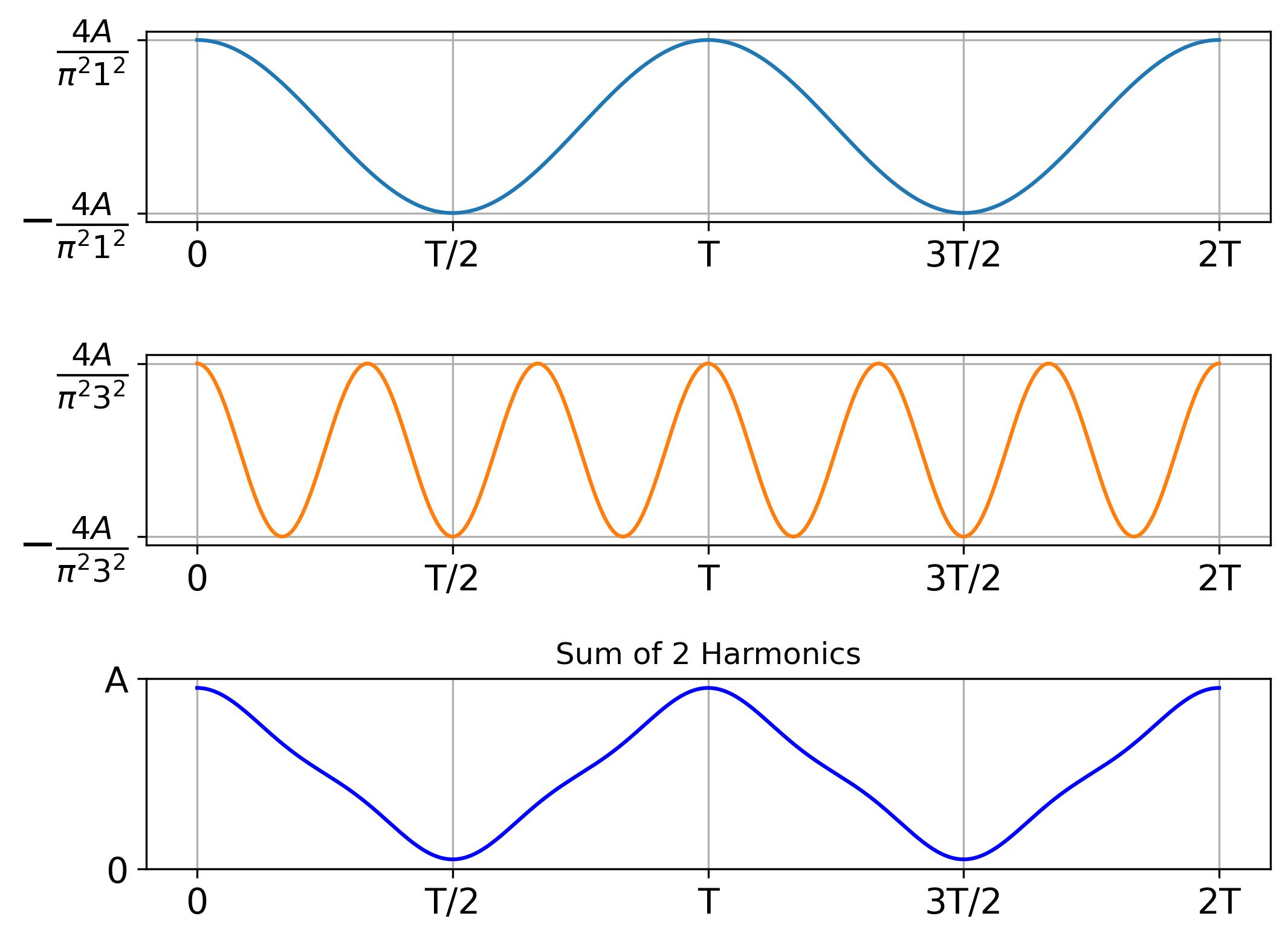
The following figure shows the first four harmonics and their sum:

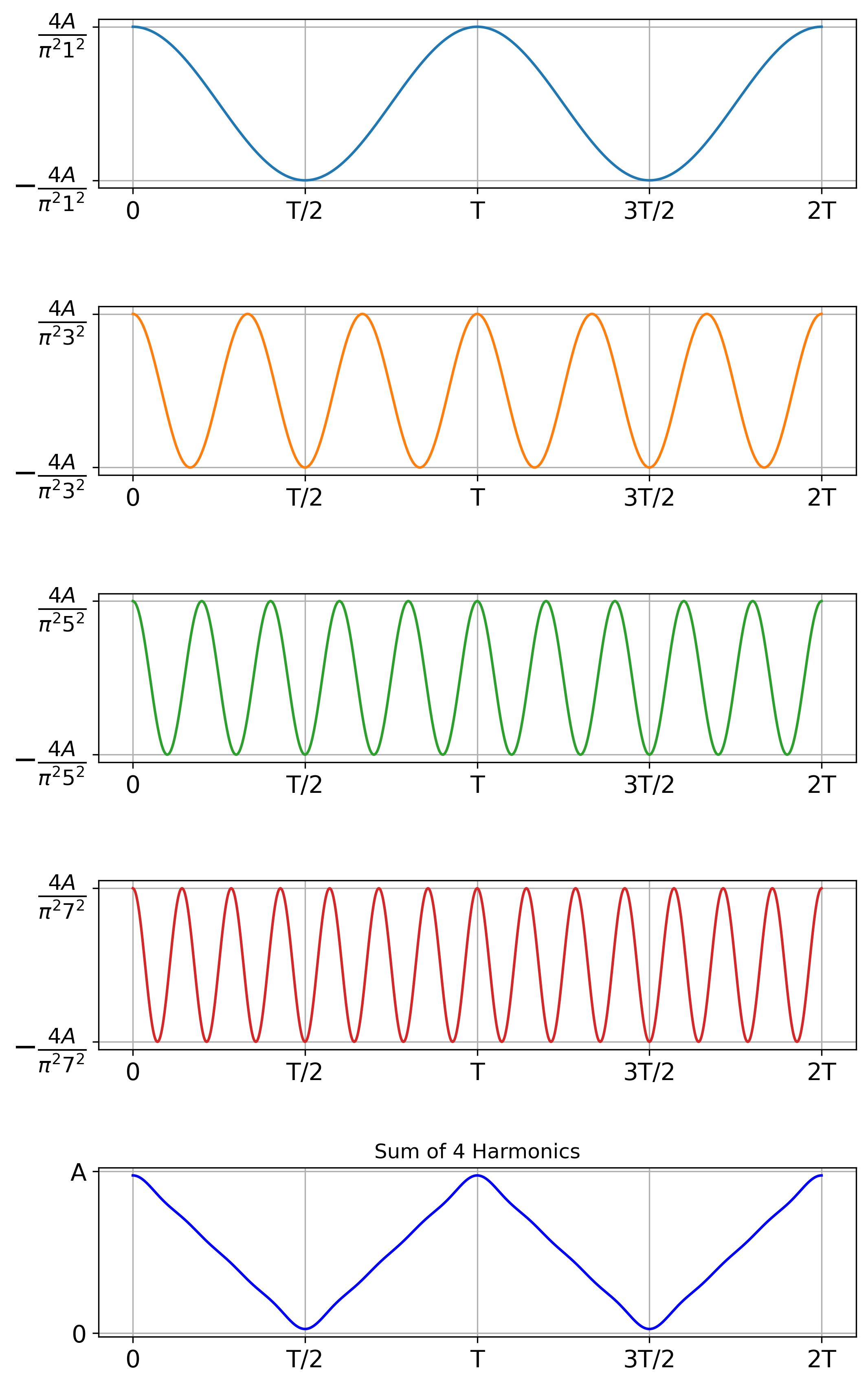
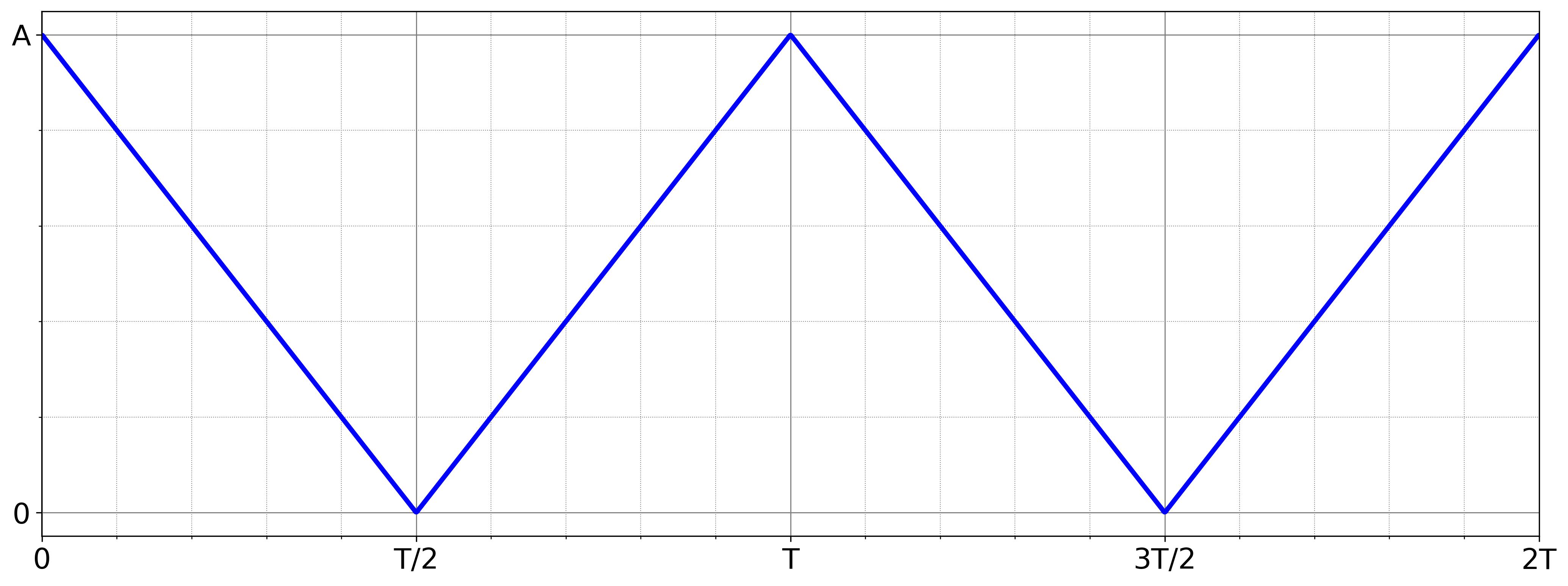
As we add more harmonics, the sum increasingly resembles the triangle wave, refining the approximation. The following figure illustrates the sum of 100 harmonics, showing how closely the resulting waveform matches the ideal triangle wave.

Even and odd functions#

Even Functions

A function \( y = x(t) \) is said to be even if it satisfies the condition:

\[ x(-t) = x(t) \quad \text{for all } t \]

The graph of an even function is always symmetric about the y-axis, meaning it is a mirror image across the vertical axis.

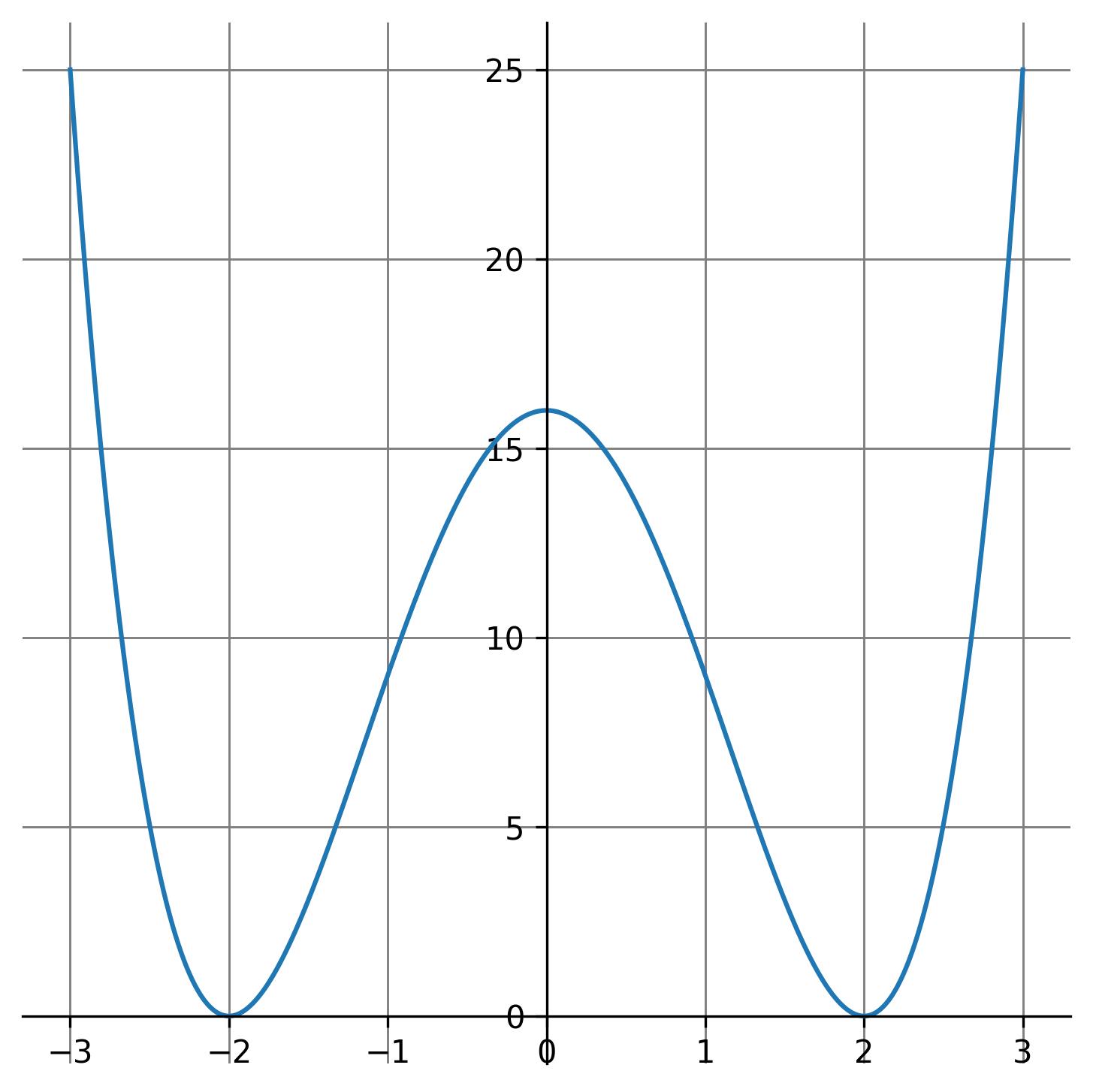
A common example of an even function is the cosine function.

For an even function \( x(t) \) defined over the interval \( -T/2 \leq t \leq T/2 \) (i.e., with period \( T \)), all sine terms in its Fourier series expansion vanish, as observed in the example of the even triangle wave. Specifically,

\[ b_m = \frac{2}{T} \int\limits_{-T/2}^{T/2} x(t) \sin\left( \frac{2\pi m}{T} t \right) dt = 0 \]

Thus, the Fourier series representation of an even function contains only cosine terms:

\[ x(t) = a_0 + \sum\limits_{m=1}^{\infty} a_m \cos\left( \frac{2\pi m}{T} t \right) \]

Odd Functions

Similarly, a function \( y = x(t) \) is said to be odd if it satisfies the condition:

\[ x(-t) = -x(t) \quad \text{for all } t \]

The graph of an odd function is always symmetric about the origin.

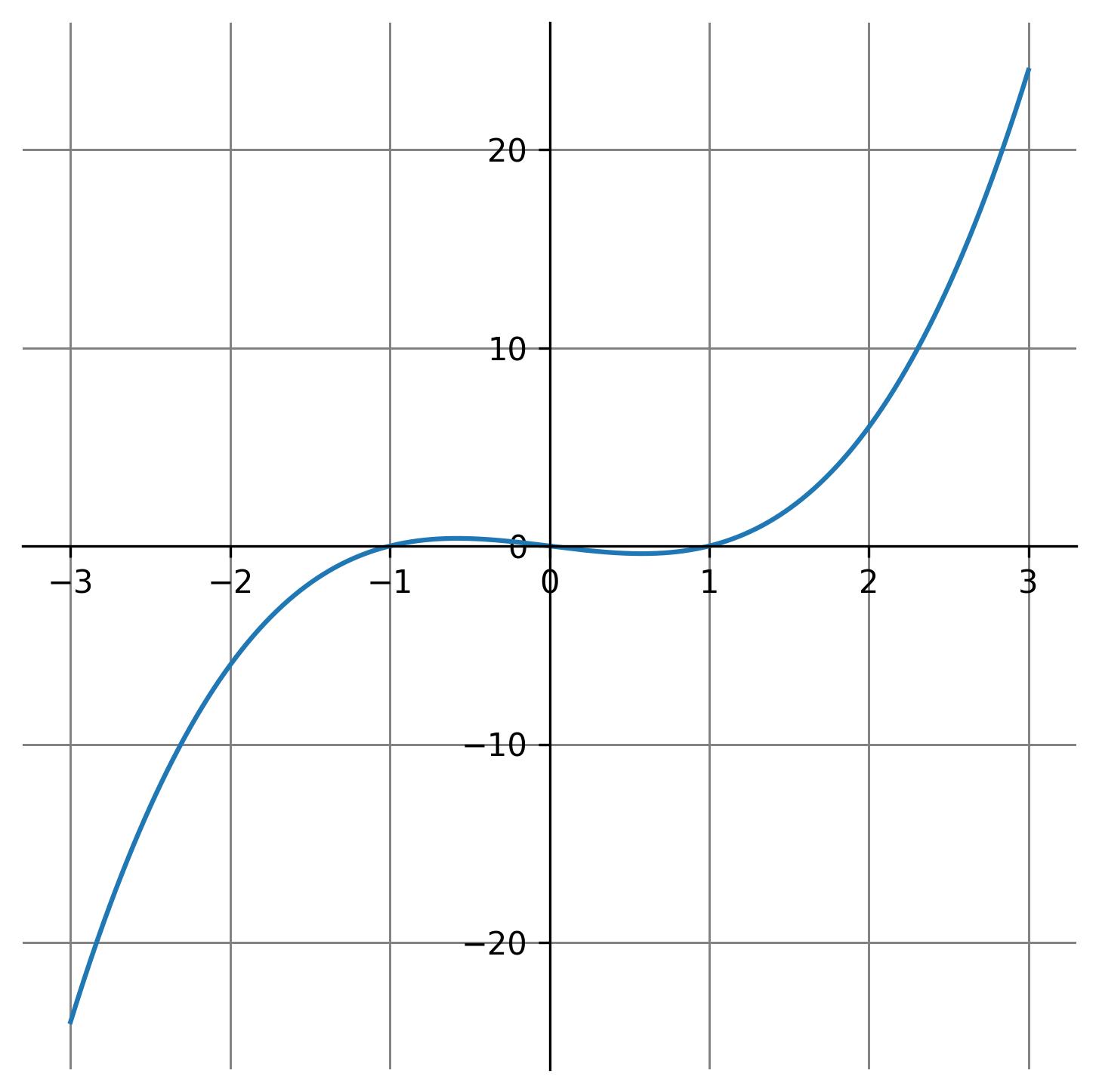
A well-known example of an odd function is the sine function.

For an odd function \( x(t) \) defined over the interval \( -T/2 \leq t \leq T/2 \) (i.e., with period \( T \)), all cosine terms in its Fourier series expansion vanish, as seen in the example of the odd square wave. Specifically,

\[ a_m = \frac{2}{T} \int\limits_{-T/2}^{T/2} x(t) \cos\left( \frac{2\pi m}{T} t \right) dt = 0 \]

Thus, the Fourier series representation of an odd function contains only sine terms:

\[ x(t) = \sum\limits_{m=1}^{\infty} b_m \sin\left( \frac{2\pi m}{T} t \right) \]

Refining Definition#

This text aims to capture the essence of the Fourier Convergence Theorem rather than delve into its full proof. The detailed proof of the theorem is beyond the scope of this text. It can be found in Section 1.2 of Partial Differential Equations and Boundary-Value Problems with Applications by M.A. Pinsky, American Mathematical Society, Third Edition, 2001.

Continuous Functions

A function \( f(x) \) is continuous over an interval \([a,b]\) if:

It is defined at every point in the interval.
The limit of \( f(x) \) as \( x \) approaches any point \( c \) within the interval exists.
The value of the function at \( c \) equals the limit as \( x \) approaches \( c \): \[ \lim_{x \to c} f(x) = f(c) \]

This means there are no breaks, jumps, or holes in the graph of \( f(x) \).

For example, the function \( f(x) = x^2 \) defined on the interval \( -\pi < x < \pi \) is continuous for all \( x \), as there are no jumps, breaks, or holes in the graph.

Piecewise Continuous Functions

While a continuous function is smooth over its entire domain, a piecewise continuous function is made up of segments that are individually continuous, but the segments may connect in ways that introduce finite jumps or breaks at specific points.

A function \( f(x) \) is piecewise continuous over an interval if:

The domain of \( f(x) \) can be divided into a finite number of subintervals.
\( f(x) \) is continuous on each subinterval (excluding endpoints).
At the boundaries of the subintervals (finite points), \( f(x) \) may have jumps or discontinuities, but these discontinuities must be finite.

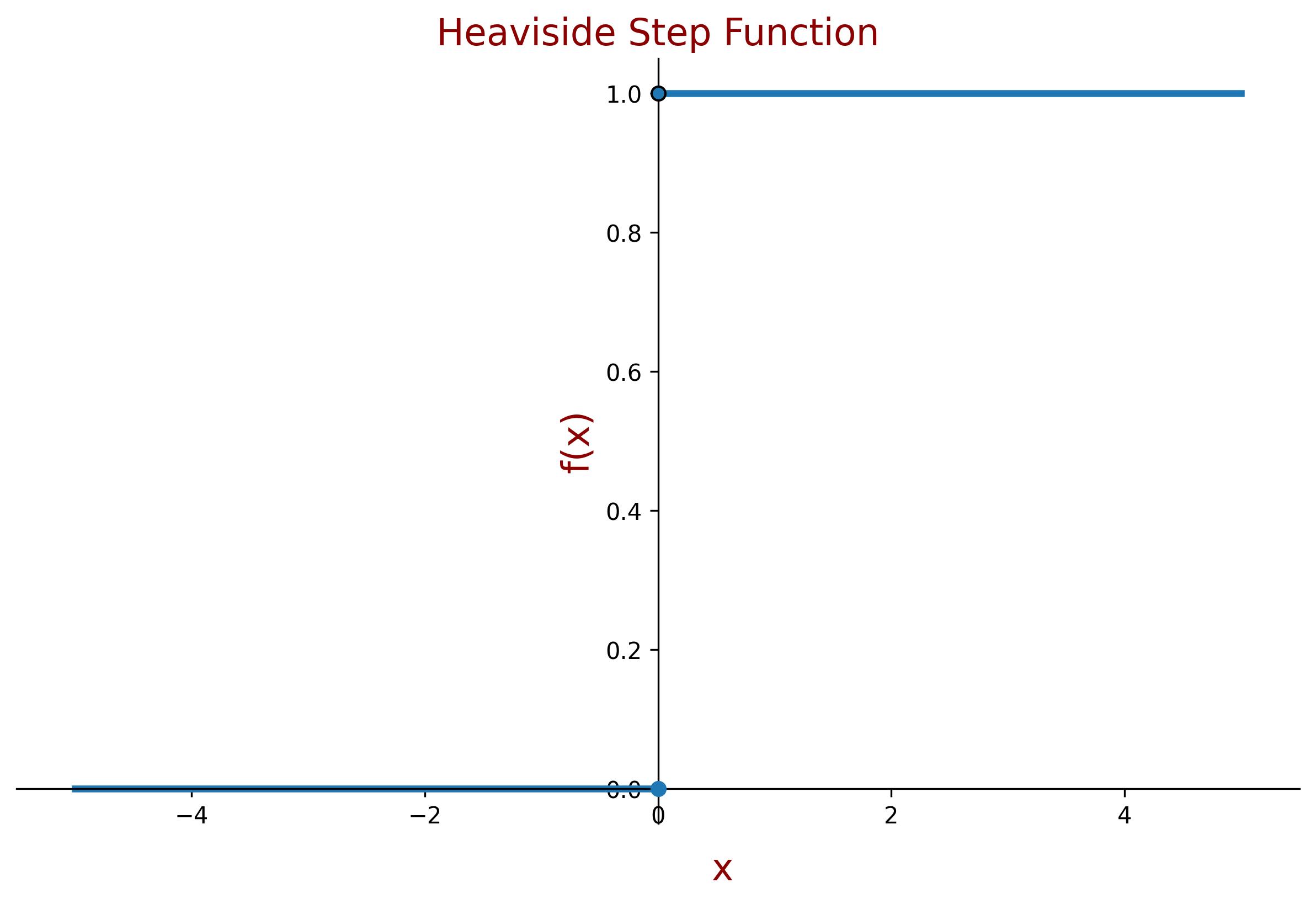
For example, consider the Heaviside step function, which takes a value of zero for negative arguments and one for positive arguments:

\[ H(x) = \begin{cases} 0, & x < 0 \\ 1, & x \geq 0 \end{cases} \]

It is continuous on the intervals \( (-\infty,0) \) and \( (0,\infty) \).
At \( x = 0 \), there is a jump discontinuity.

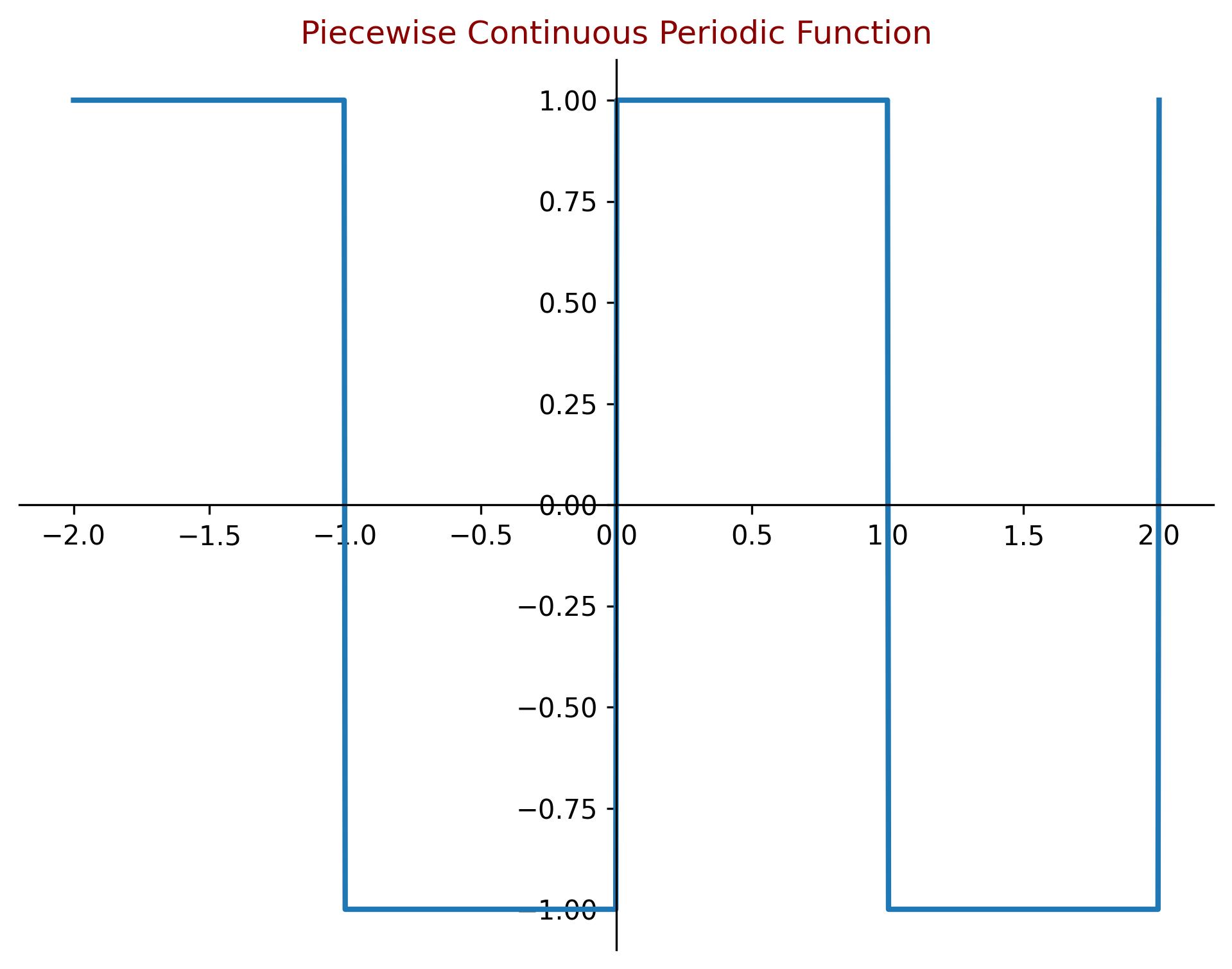
A classic square wave function is an example of a piecewise continuous periodic function:

\[ f(x) = \begin{cases} 1, & 0 \leq x < T/2 \\ -1, & T/2 \leq x < T \end{cases} \]

The function is continuous within each subinterval \( [0,T/2) \) and \( [T/2,T) \).
It has jump discontinuities at \( x = nT \) and \( x = nT + T/2 \), where \( n \) is an integer.

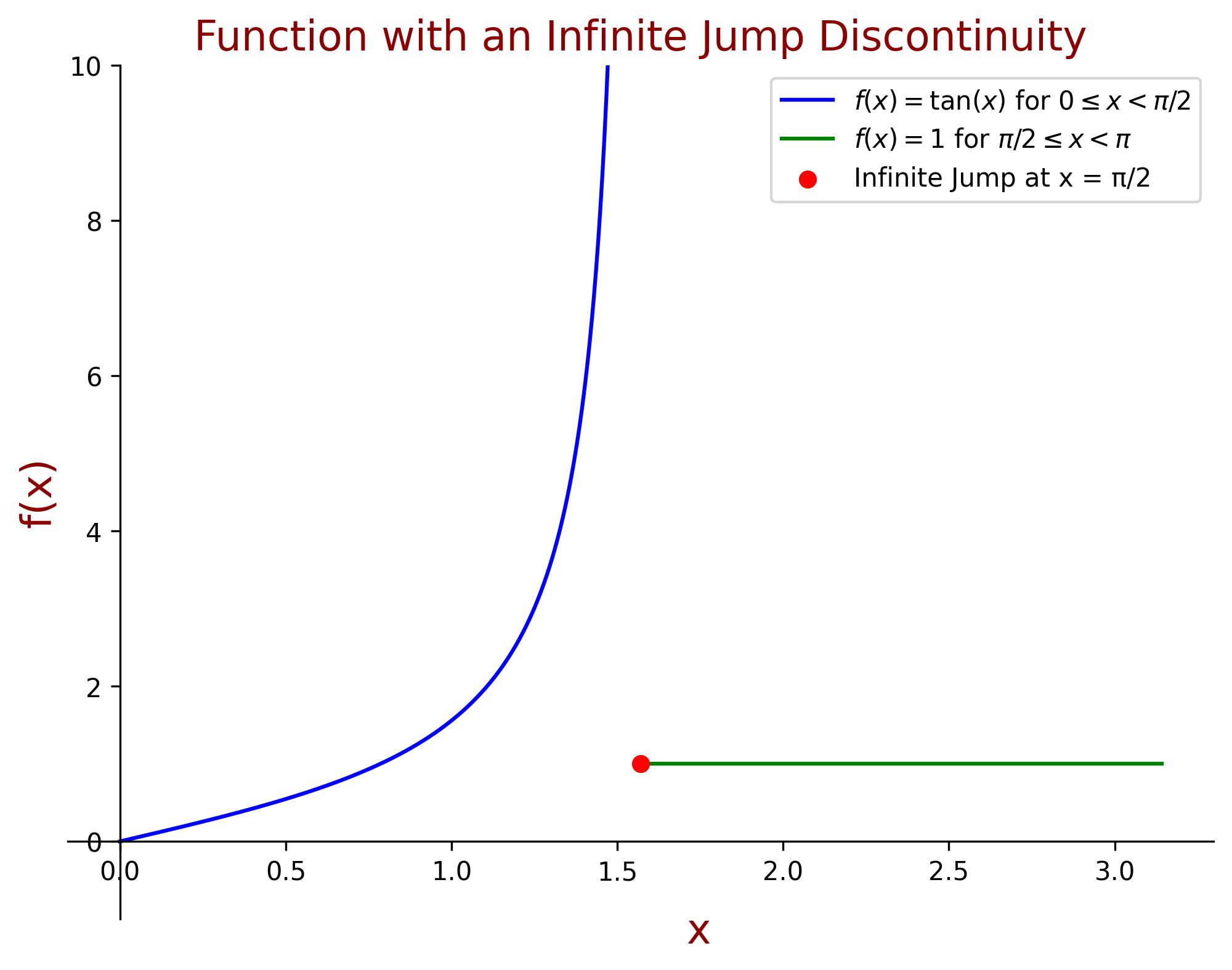
An example of a function that is not piecewise continuous due to an infinite jump at a certain point is:

\[ f(x) = \begin{cases} \tan(x), & 0 \leq x < \pi/2 \\ 1, & \pi/2 \leq x < \pi \end{cases} \]

The function \( f(x) \) is defined in two pieces: \( \tan(x) \) for \( 0 \leq x < \pi/2 \), and a constant value \( 1 \) for \( \pi/2 \leq x < \pi \).

However, as \( x \to \pi/2^- \), \( \tan(x) \to \infty \), meaning there is an infinite jump discontinuity at \( x = \pi/2 \).

Since piecewise continuity requires only finite jumps, \( f(x) \) is not piecewise continuous.

Piecewise Smooth Functions

If both \( f(x) \) and \( f'(x) \) are continuous or piecewise continuous, then \( f \) is called piecewise smooth.

This means that the graphs of \( f(x) \) and \( f'(x) \) may have only finitely many finite jumps.

For example, the function

\[ f(x) = \begin{cases} \sin(x), & -\pi < x < 0 \\ x^2, & 0 \leq x < \pi \end{cases} \]

is piecewise smooth because:

\( f(x) \) is continuous over the interval \( -\pi < x < \pi \), as both \( \sin(x) \) and \( x^2 \) are continuous functions, and they match at \( x = 0 \).

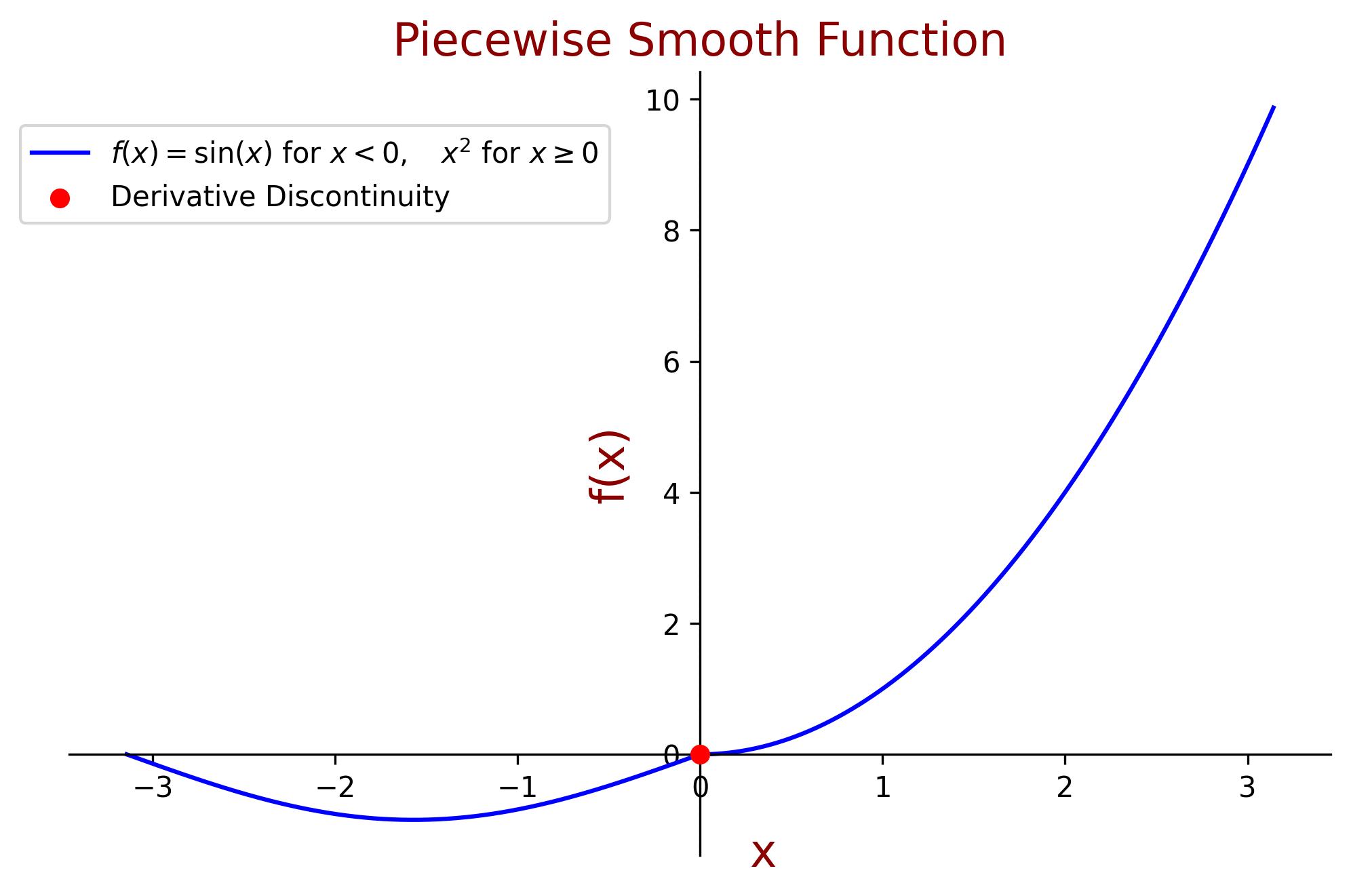
The derivative of \( f(x) \):

\[ f'(x) = \begin{cases} \cos(x), & -\pi < x < 0 \\ 2x, & 0 \leq x < \pi \end{cases} \]

It is discontinuous at \( x = 0 \), however, the jump of \( f'(x) \) at \( x = 0 \) is finite, therefore \( f'(x) \) is piecewise continuous.

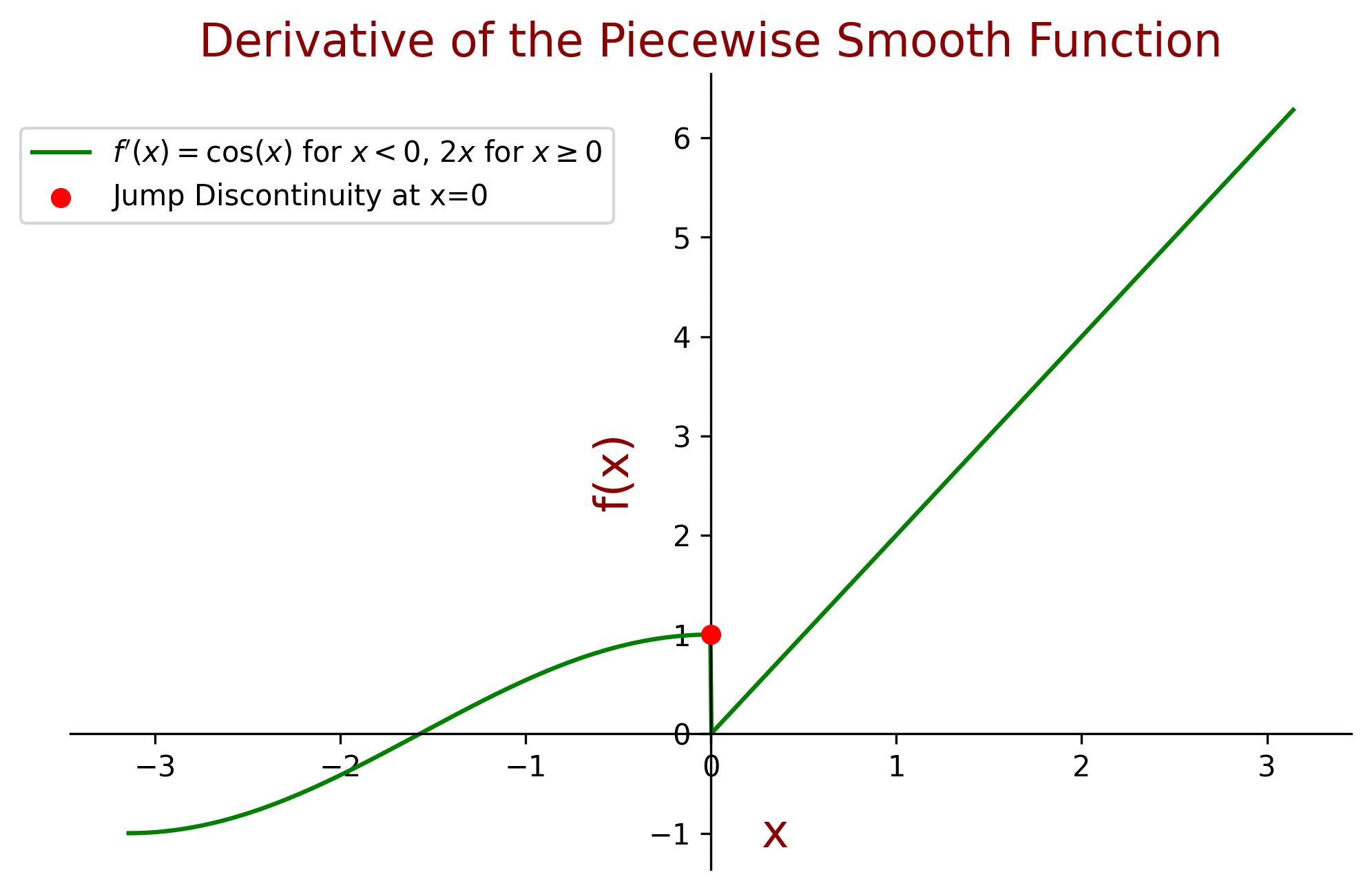
The derivative of the Piecewise Smooth Functions

Since \( f(x) \) is continuous and \( f'(x) \) is piecewise continuous, the function \( f(x) \) is piecewise smooth.

Convergence

The Fourier series of a function \( f(x) \) at \( x = x_0 \) converges to:

\[ \frac{1}{2} \left( f(x_0^-) + f(x_0^+) \right) \]

where:

\[ f(x_0^-) = \lim_{x \to x_0^-} f(x) \] \[ f(x_0^+) = \lim_{x \to x_0^+} f(x) \]

If \( x = x_0 \) is a point of continuity of \( f(x) \), the Fourier series converges to \( f(x_0) \).
If \( x = x_0 \) is a point of discontinuity of \( f(x) \), the Fourier series converges to the average of the left- and right-hand limits of \( f(x) \) at \( x = x_0 \).

For a square wave, the Fourier series converges to 0 at points of discontinuity:

\[ f(nT/2) = \frac{1}{2} (-1 + 1) = 0 \]

This illustrates that the Fourier series does not necessarily converge to the function’s value at discontinuities but rather to the midpoint of the jump.

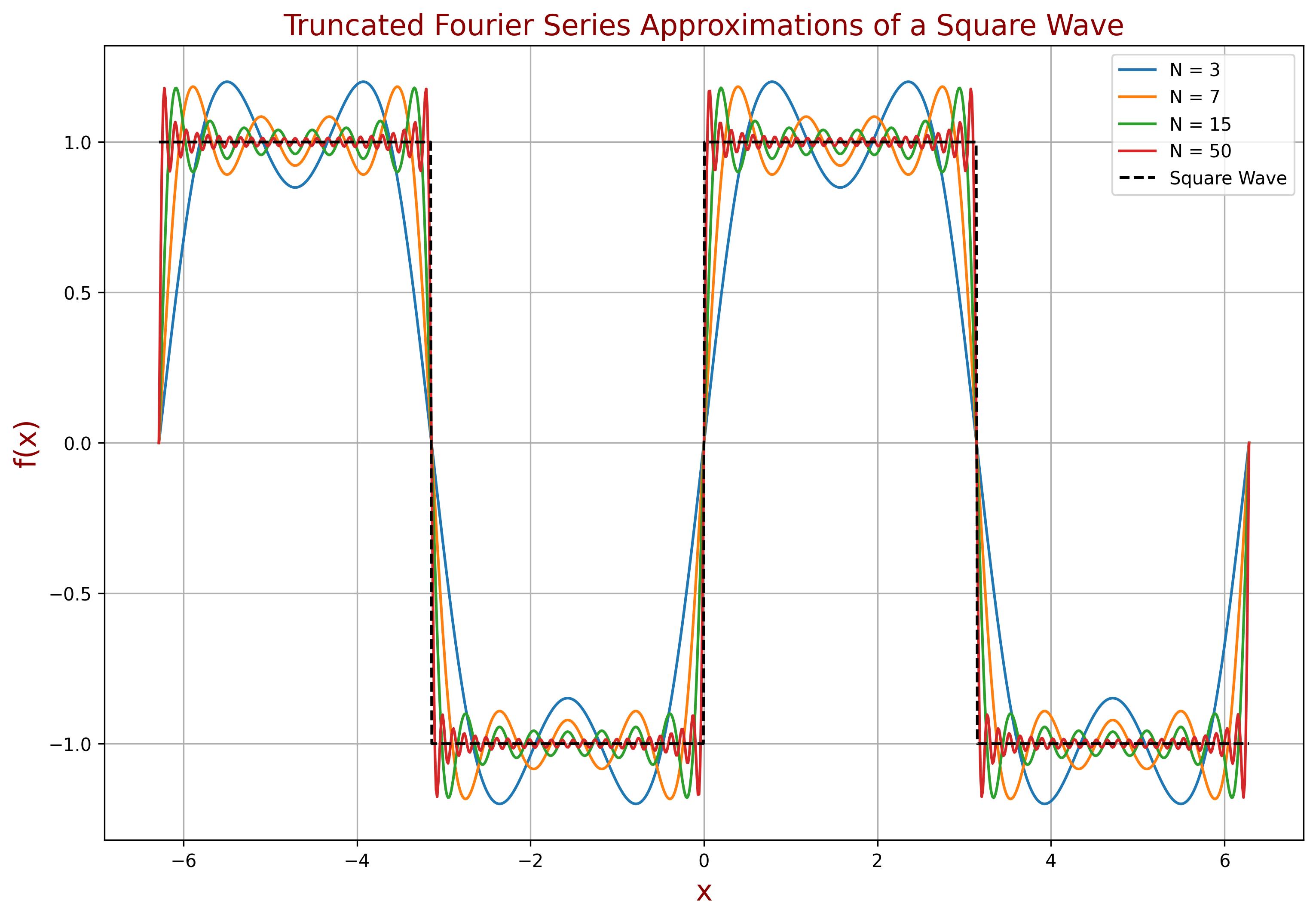
Gibbs Phenomenon#

In the square wave example, we observe an overshoot near discontinuity points, where \( f(x) \) does not converge to \( f(x_0) \).

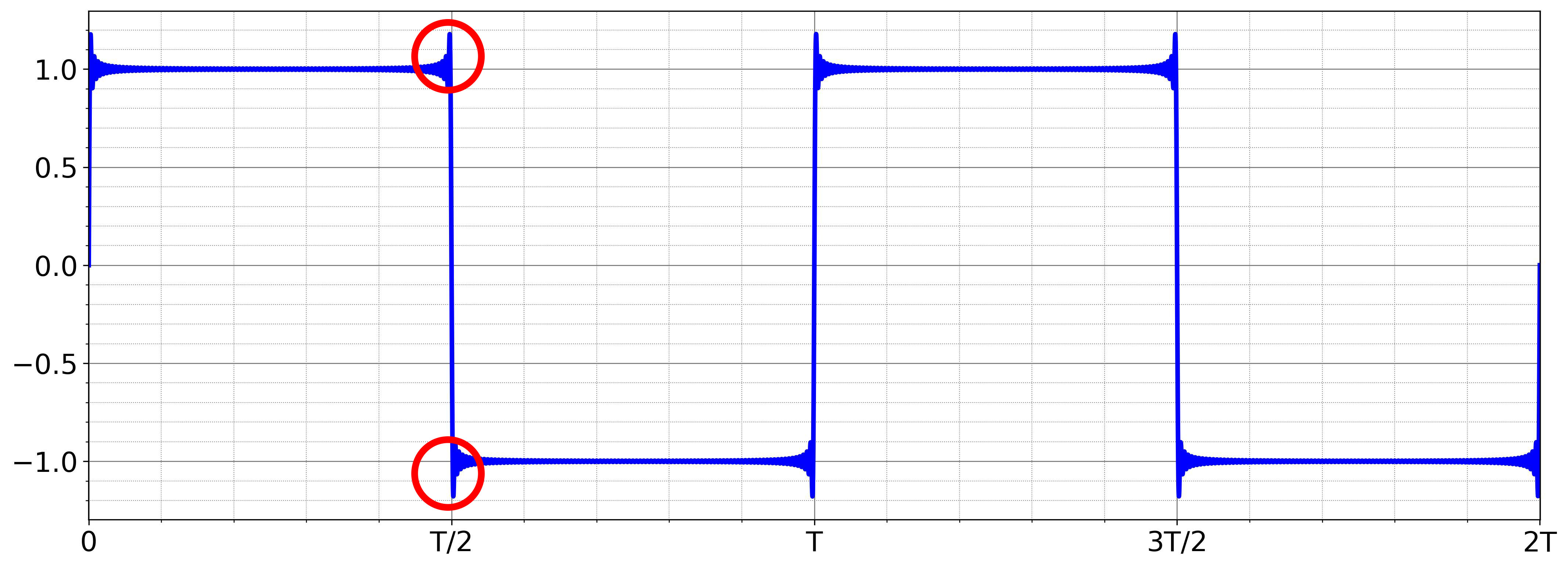
This overshoot is known as the Gibbs phenomenon, first discovered by Henry Wilbraham in 1848. However, it became widely associated with Josiah Willard Gibbs, who analyzed it in more detail and published his findings nearly 50 years later.

Theorem

If \( f(x) \) is piecewise smooth on \([-T/2,T/2]\), then the overshoot of its truncated Fourier series of \( f(x) \) at a discontinuity \( x_0 \) (i.e., the Gibbs phenomenon) is approximately 9% of the jump in function values:

\[ \text{Overshoot} \approx 0.09 \left( f(x_0^-) + f(x_0^+) \right) \]

The proof of the theorem is beyond the scope of this text.

The figure below illustrates the Gibbs phenomenon in the Fourier Series approximation of a square wave, showing how the approximation behaves for different numbers of terms (\( N \)).