Appendix B

Integrals of Sinusoidal Products#

This appendix contains the derivations of three integrals utilized in various book sections.

Where:

• $m$ and $n$ are integers
• $T$ is a full period time corresponding to an angle of $2\pi$
• $\omega$ is the angular frequency
• $t$ is time

$\omega t$ represents an angle.

We assume that all sine and cosine functions are periodic over period $T$. A periodic signal is defined as a signal that repeats itself at regular intervals over time. Mathematically, a signal $x(t)$ is periodic if there exists a positive constant $T$, known as the period, such that:

A signal is classified as aperiodic if it does not meet these conditions.

The fundamental frequency of a periodic signal is given by:

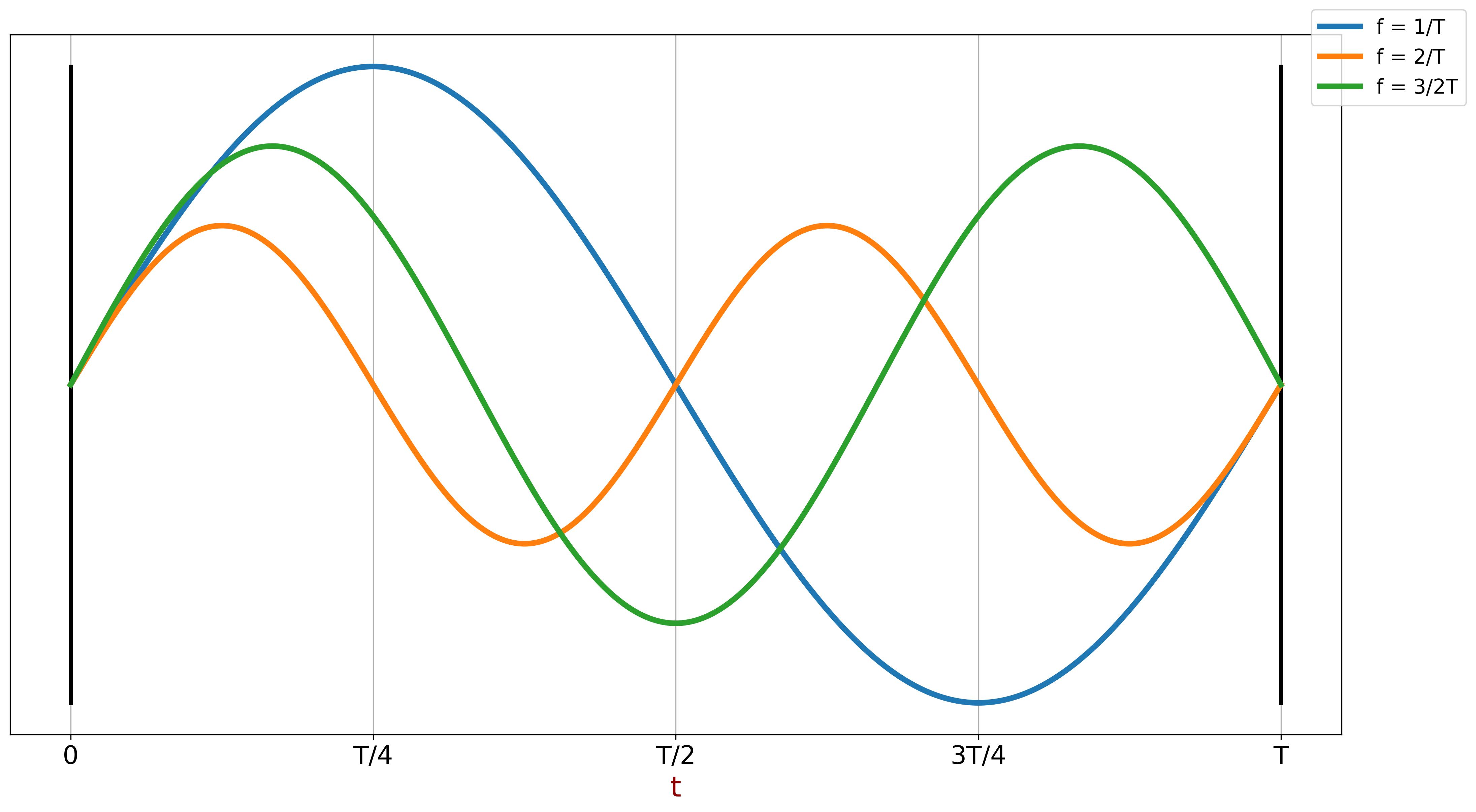
Additionally, sine functions with frequencies that are integer multiples of $f_0$ (i.e., $k{f}_0$ for $k\in \mathbb{Z}$) remain periodic over period $T$. Notice that the green sine wave is aperiodic, as it completes 1.5 cycles within the interval $T$, meaning it does not repeat itself consistently over $T$.

The integral of sine and cosine product#

Applying the trigonometric identity:

First integral solution:

Second integral solution:

The integral of two sines product#

$${\displaystyle \underset{0}{\overset{T}{\int }}\sin (m\omega t)\sin (n\omega t)dt}$$

Let us apply the trigonometric identity for the product of two sines:

For $m=n$:

For $m\ne n$

First integral solution:

Second integral solution:

The integral of two cosines product#

$${\displaystyle \underset{0}{\overset{T}{\int }}\cos (m\omega t)\cos (n\omega t)dt}$$

Let us apply the trigonometric identity for the product of two cosines:

For $m=n$:

For $m\ne n$:

First integral solution:

Second integral solution: