DFT#
The Discrete Fourier Transform (DFT) can be considered a counterpart to the Fourier Series in the discrete domain. While the Fourier Series is used for Fourier analysis of periodic or time-limited signals in the continuous domain, the DFT serves the same purpose for signals in the discrete domain.
Unlike the Fourier Series, which is primarily a theoretical tool, the DFT is a practical tool widely used for the spectral analysis of arbitrarily sampled signals. Formalized in the mid-20th century, the DFT provided a direct method for computing the Fourier transform of discrete signals. However, its computational complexity posed a significant challenge.
In 1965, James Cooley and John Tukey introduced the Fast Fourier Transform (FFT), an algorithm that dramatically reduced the computational cost of the DFT. This breakthrough enabled real-time digital signal processing (DSP) and revolutionized applications in communications, imaging, radar, and beyond.
Today, the DFT (especially in its FFT-accelerated form) is at the core of nearly all modern DSP applications. It is not just a computational tool but a fundamental concept for analyzing and manipulating signals in an increasingly digital world.
Note
This chapter presents a real-number-based explanation of the Discrete Fourier Transform (DFT), making it clear and intuitive for beginners. We will revisit the topic later, after introducing complex numbers.
For the avoidance of doubt, you do not need to understand complex numbers to perform the DFT. However, the complex representation of the DFT is more elegant, compact, and convenient.
From Fourier Series to DFT#
The following figure illustrates the correlation-based concept of spectral decomposition used in the Fourier Series.
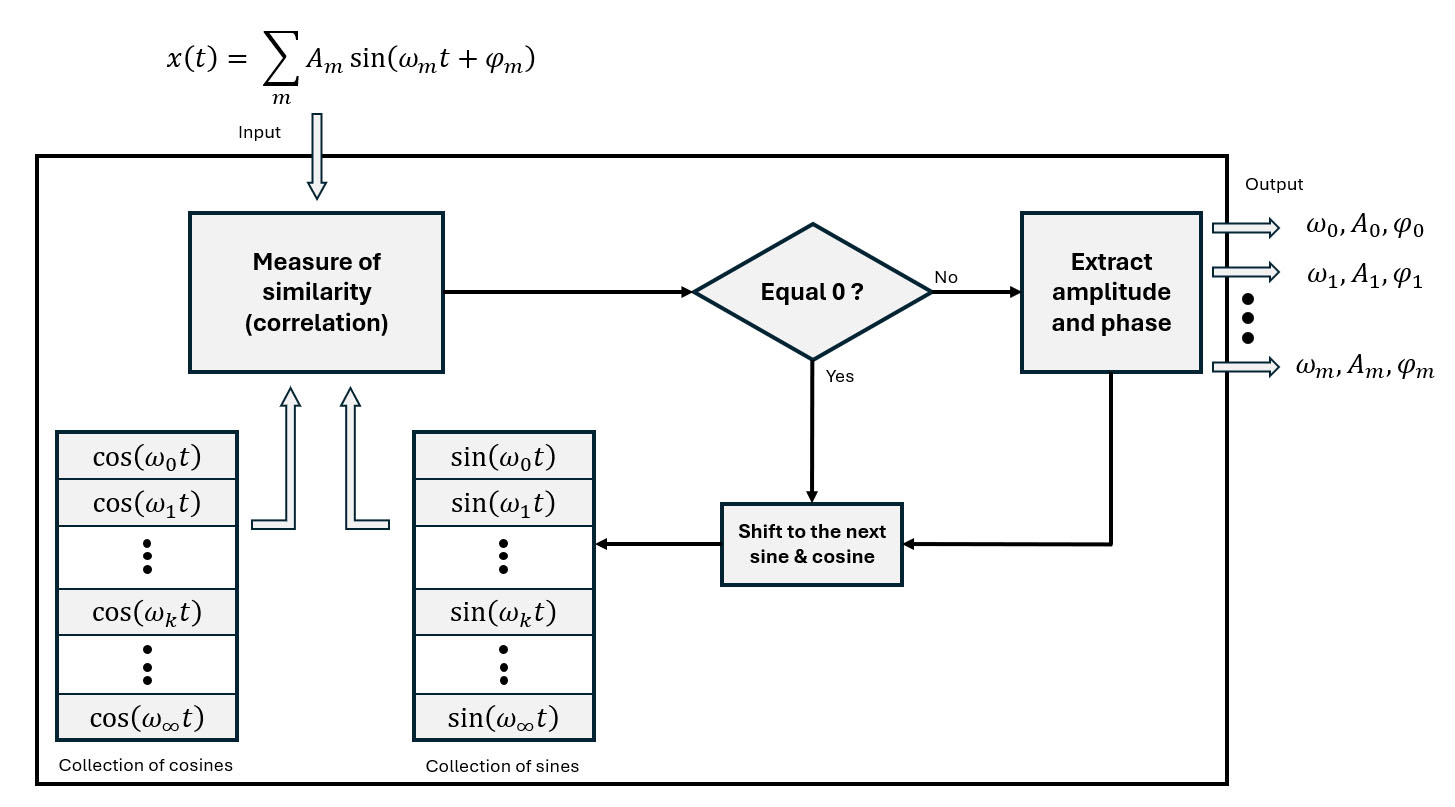
Now, let’s adapt this method for the discrete domain.
The input signal#
In digital systems, the input signal is discrete, typically obtained by sampling a continuous signal using an Analog-to-Digital Converter (ADC). As we saw in the previous chapter, a periodic sinusoid with frequency \( f_k \) can be expressed as:
\[ x_k = \sin\left( \frac{2\pi k}{N} n \right), \quad 0 \leq k \leq N-1 \]
Given an arbitrary signal consisting of \( M \) distinct sinusoids and a constant component (DC bias), where all sinusoids are periodic over a time interval \( T \), the continuous-domain representation is:
\[ x(t) = \sum_{m=0}^{M} A_m \sin\left( \omega_m t + \phi_m \right) \]
After sampling, the discrete-domain representation becomes:
\[ x(n) = \sum_{m=0}^{M} A_m \sin\left( \frac{2\pi m}{N} n + \phi_m \right) \]
Predefined sines and cosines#
In the Fourier Series, we correlate the input signal with an infinite set of sine and cosine functions. While this is useful for theoretical analysis, it is impractical in real-world applications due to finite memory and processing time. Even if infinite resources were available, the number of sine and cosine components that can be meaningfully extracted is limited by the Nyquist-Shannon Sampling Theorem:
Unlike the continuous Fourier Series, which involves an infinite set of harmonics, the discrete version is limited to half the sampling rate. In the previous chapter, we derived the range for discrete frequencies \( f_k \):
\[ 0 \leq k \leq N - 1 \]
The periodic sine wave with frequency \( f_k \) is expressed as:
\[ x_s[n] = \sin\left( \frac{2\pi k}{N} n \right) \]
Similarly, the periodic cosine wave with frequency \( f_k \) is:
\[ x_c[n] = \cos\left( \frac{2\pi k}{N} n \right) \]
The relation between the discrete frequencies and corresponding analog frequencies is given by:
\[ f = \begin{cases} \dfrac{k}{N} f_s, & 0 \leq k \leq \dfrac{N}{2} - 1 \\ \\ \dfrac{k - N}{N} f_s, & \dfrac{N}{2} \leq k \leq N - 1 \end{cases} \]
Discrete Fourier Coefficients#
In the continuous domain, the Fourier series coefficients are defined as:
In the discrete domain, the Fourier series coefficients take the form:
To ensure consistency, we introduce the \(b_0\) term and modify \(a_0\) by explicitly including the cosine term and using a normalization factor of \( \dfrac{2}{N} \):
\[ a_0 = \frac{2}{N} \sum_{n=0}^{N-1} x(n) \cos\left( \frac{2\pi \cdot 0}{N} n \right) \]
\[ b_0 = \frac{2}{N} \sum_{n=0}^{N-1} x(n) \sin\left( \frac{2\pi \cdot 0}{N} n \right) \]
Since:
- \( \cos\left( \dfrac{2\pi \cdot 0}{N} n \right) = 1 \), it doesn’t affect \(a_0\)
- \( \sin\left( \dfrac{2\pi \cdot 0}{N} n \right) = 0 \), implying \(b_0 = 0\)
We obtain the final discrete Fourier series coefficients:
These equations represent the real-valued Discrete Fourier Transform (DFT). Later, we will introduce the complex form of the DFT.
Using the computed coefficients, the original discrete signal can be reconstructed as:
DFT in matrix form#
Expressing the Discrete Fourier Transform (DFT) in matrix form is more practical because it allows for a compact representation of the transformation as a matrix-vector multiplication. This makes it easier to analyze the structure of the DFT and leverage efficient computational techniques. By formulating the DFT in matrix form, we can take advantage of linear algebra operations, enabling more efficient implementations with numerical libraries.
The Fourier coefficients can be determined through matrix-vector multiplication as follows:
\[ \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{N-1} \end{bmatrix} = \frac{2}{N} \left[ \begin{array}{cccc} \cos\left(\frac{2\pi \cdot 0}{N} \cdot 0\right) & \cos\left(\frac{2\pi \cdot 0}{N} \cdot 1\right) & \cdots & \cos\left(\frac{2\pi \cdot 0}{N}(N-1)\right) \\ \cos\left(\frac{2\pi \cdot 1}{N} \cdot 0\right) & \cos\left(\frac{2\pi \cdot 1}{N} \cdot 1\right) & \cdots & \cos\left(\frac{2\pi \cdot 1}{N}(N-1)\right) \\ \vdots & \vdots & \ddots & \vdots \\ \cos\left(\frac{2\pi (N-1)}{N} \cdot 0\right) & \cos\left(\frac{2\pi (N-1)}{N} \cdot 1\right) & \cdots & \cos\left(\frac{2\pi (N-1)}{N}(N-1)\right) \end{array} \right] \cdot \begin{bmatrix} x(0) \\ x(1) \\ \vdots \\ x(N-1) \end{bmatrix} \]
The matrix element is: \( \cos\left( \dfrac{2\pi k}{N} n \right) \)
Similarly:
\[ \begin{bmatrix} b_0 \\ b_1 \\ \vdots \\ b_{N-1} \end{bmatrix} = \frac{2}{N} \left[ \begin{array}{cccc} \sin\left(\frac{2\pi \cdot 0}{N} \cdot 0\right) & \sin\left(\frac{2\pi \cdot 0}{N} \cdot 1\right) & \cdots & \sin\left(\frac{2\pi \cdot 0}{N}(N-1)\right) \\ \sin\left(\frac{2\pi \cdot 1}{N} \cdot 0\right) & \sin\left(\frac{2\pi \cdot 1}{N} \cdot 1\right) & \cdots & \sin\left(\frac{2\pi \cdot 1}{N}(N-1)\right) \\ \vdots & \vdots & \ddots & \vdots \\ \sin\left(\frac{2\pi (N-1)}{N} \cdot 0\right) & \sin\left(\frac{2\pi (N-1)}{N} \cdot 1\right) & \cdots & \sin\left(\frac{2\pi (N-1)}{N}(N-1)\right) \end{array} \right] \cdot \begin{bmatrix} x(0) \\ x(1) \\ \vdots \\ x(N-1) \end{bmatrix} \]
The matrix element is: \( \sin\left( \dfrac{2\pi k}{N} n \right) \)
Parameters extraction#
As defined at the beginning of the Fourier Series chapter:
\[ b_k = A_k \cos\left( \phi_k \right) \]
\[ a_k = A_k \sin\left( \phi_k \right) \]
The coefficients \( a_k \) and \( b_k \) serve as weights that encode the amplitude and phase of the frequency component \( f_k \).
To extract the amplitude \( A_k \) of the frequency component \( f_k \), we use:
\[ \sqrt{a_k^2 + b_k^2} = \sqrt{\left(A_k \sin\left( \phi_k \right)\right)^2 + \left(A_k \cos\left( \phi_k \right)\right)^2} = A_k \sqrt{\sin^2\left( \phi_k \right) + \cos^2\left( \phi_k \right)} \]
Since \( \sin^2\left( \phi_k \right) + \cos^2\left( \phi_k \right) = 1 \), this simplifies to:
To determine the phase \( \phi_k \), we take the ratio:
\[ \frac{a_k}{b_k} = \frac{A_k \sin\left( \phi_k \right)}{A_k \cos\left( \phi_k \right)} = \frac{\sin\left( \phi_k \right)}{\cos\left( \phi_k \right)} = \tan\left( \phi_k \right) \]
Solving for \( \phi_k \):
The following figure illustrates the correlation-based spectral decomposition used in the DFT:
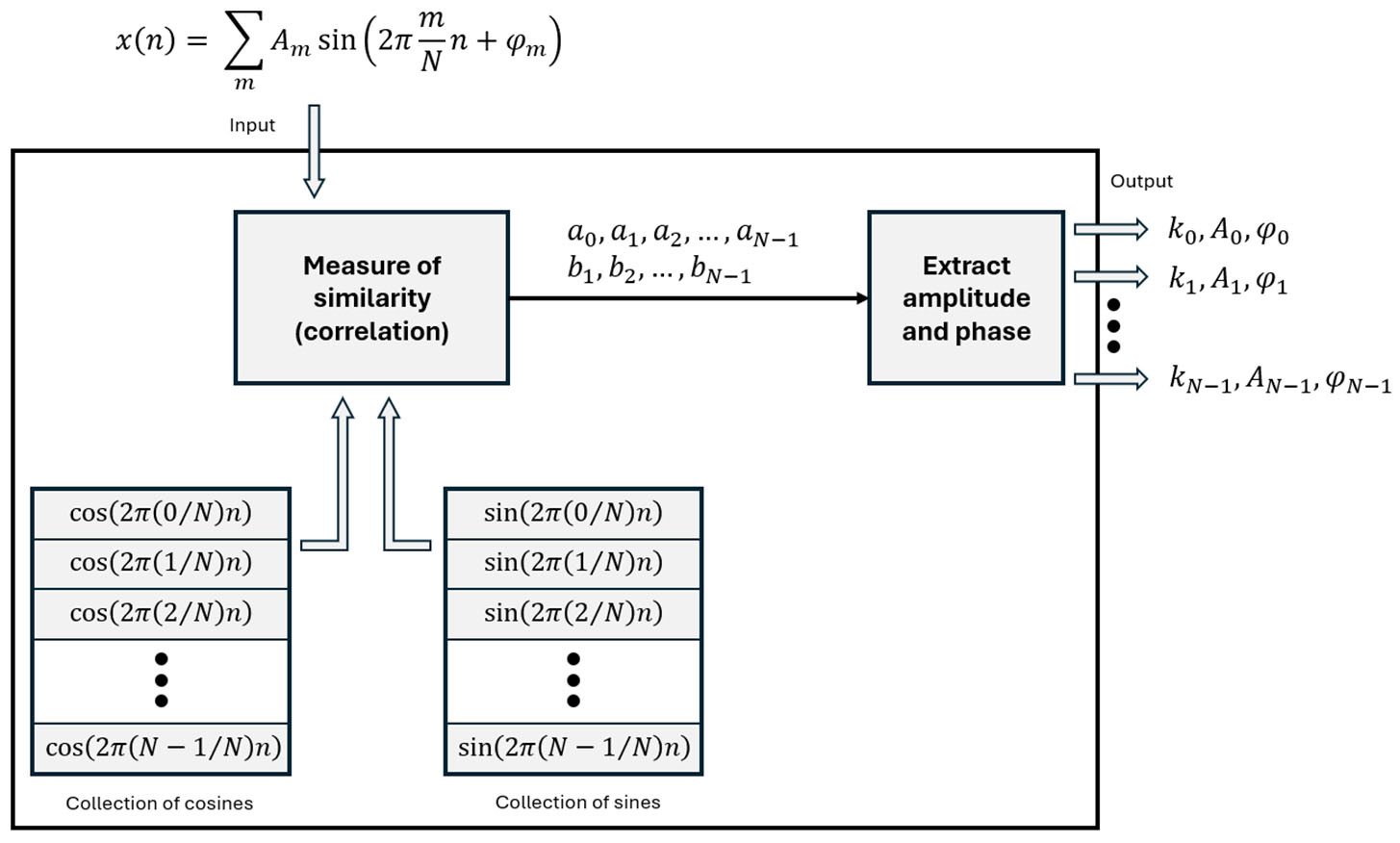
To better understand this concept, let's work through an example.