Fourier Series#
Consider an arbitrary signal consisting of \( M \) distinct sinusoids and a constant component (DC bias). All sinusoids are periodic over time interval \( T \). This signal can be mathematically expressed as:
\[ x(t) = \sum\limits_{m=0}^{M} A_m \sin(\omega_m t + \phi_m) \]We begin by examining the constant component (\( m=0 \)):
\[ A_0 \sin(\omega_0 t + \phi_0) = A_0 (u \cdot \sin(\omega_0 t) + v \cdot \cos(\omega_0 t)) \]For the constant component, the frequency is zero (\( \omega_{m=0} = 0 \)):
\[ A_0 (u \cdot 0 + v \cdot 1) = A_0 v = A_0 \sin(\phi) \]Thus, we obtain a constant term. In literature, this constant term is often represented as \( a_0 \):
\[ a_0 = A_0 \sin(\phi) \]We will rewrite the signal as:
\[ x(t) = a_0 + \sum\limits_{m=1}^{M} A_m \sin(\omega_m t + \phi_m) \]Let’s express the signal as a combination of sine and cosine terms:
\[ x(t) = a_0 + \sum\limits_{m=1}^{M} A_m (u_m \sin(\omega_m t) + v_m \cos(\omega_m t)) \]Define the following parameters:
\[ b_m = A_m u_m = A_m \cos(\phi_m) \] \[ a_m = A_m v_m = A_m \sin(\phi_m) \]The signal can be described as a constant part and a weighted sum of sines and cosines:
This allows us to represent the arbitrary signal consisting of \( M \) distinct sinusoids and a constant component as a constant term plus a weighted sum of sine and cosine functions.
The equation above is known as the Fourier Series equation.
The coefficients \( a_0, a_1, \dots, a_m, b_1, \dots, b_m \) are known as Fourier Coefficients.
The Fourier Series represents a signal as a sum of sinusoids that are periodic over the time interval \( T \). The frequencies of these sinusoids are integer multiples of the fundamental frequency \( f_1 = \dfrac{1}{T} \). Thus, the Fourier Series can be expressed as:
Where \( \omega_m = \dfrac{2\pi m}{T} \).
Fourier Analysis concept#
The Fourier Series is a foundational tool for the theoretical analysis of periodic or time-limited continuous signals.
Assuming the input signal \( x(t) \) is composed of a constant term, \( a_0 \), and a combination of sinusoids where the weights of the cosine and sine terms are \( a_m \) and \( b_m \), respectively, we can determine its frequency content by extracting the Fourier coefficients \( a_1, \dots, a_M \), \( b_1, \dots, b_M \).
To extract these coefficients, we compute the measure of similarity (or correlation) between the signal and a comprehensive set of sines and cosines with varying frequencies. When a particular sine or cosine matches a signal component, the correlation yields a non-zero result.
Extracting \(a_0 \):
The \(a_0 \) coefficient represents the constant component (DC bias) of the signal. To find \(a_0 \), we look at the correlation between \( x(t) \) and \( \cos(\omega_0 t) \) when \( \omega_0 = 0 \), which gives the mean of \( x(t) \):
\[ \int\limits_0^T x(t) \cos(0) \, dt = \int\limits_0^T x(t) \, dt = \int\limits_0^T \left( a_0 + \sum\limits_{m=1}^{M} (b_m \sin(\omega_m t) + a_m \cos(\omega_m t)) \right) dt \]Expanding this integral, we get:
\[ \color{green}{a_0 \int\limits_0^T dt} \color{#222832}{\ +\ } \color{red}{\sum\limits_{m=1}^{M} b_m \int\limits_0^T \sin(\omega_m t) dt} \color{#222832}{\ +\ } \color{blue}{\sum\limits_{m=1}^{M} a_m \int\limits_0^T \cos(\omega_m t) dt} \]Since the sine and cosine terms are periodic, their integrals over a full period \( T \) are zero:
\[ \color{red}{\int\limits_0^T \sin(\omega_m t) dt = -\frac{1}{\omega_m} \left[ \cos(\omega_m t) \right]_0^T = -\frac{1}{\omega_m} (1-1) = 0} \]Similarly, the integration of cosine over a full period is also zero:
\[ \color{blue}{\int\limits_0^T \cos(\omega_m t) dt = \frac{1}{\omega_m} \left[ \sin(\omega_m t) \right]_0^T = \frac{1}{\omega_m} (0-0) = 0} \]This simplifies to only the term containing\( a_0 \):
\[ \color{green}{a_0 \int\limits_0^T dt = a_0 [t]_0^T = a_0 T - a_0 (0) = a_0 T} \] \[ \int\limits_0^T x(t) \cos(\omega_0 t) dt = a_0 T \]Solving for \( a_0 \):
Thus, the constant component \( a_0 \) of the signal is found by calculating the correlation between \( x(t) \) and \( \cos(0) \) divided by the signal period \( T \).
Note that the correlation between \( x(t) \) and \( \sin(\omega_0 t) \), for \( \omega_0=0 \) is 0, meaning there is no \( b_0 \) coefficient:
\[ \int\limits_0^T x(t) \sin(0) dt = 0 \]Geometric Interpretation of the Result:
The integral \( \int\limits_0^T x(t) dt \) represents the area under \( x(t) \). If \( a_0 = 0 \) (no constant component), the positive and negative areas of a periodic signal will cancel each other, resulting in zero.
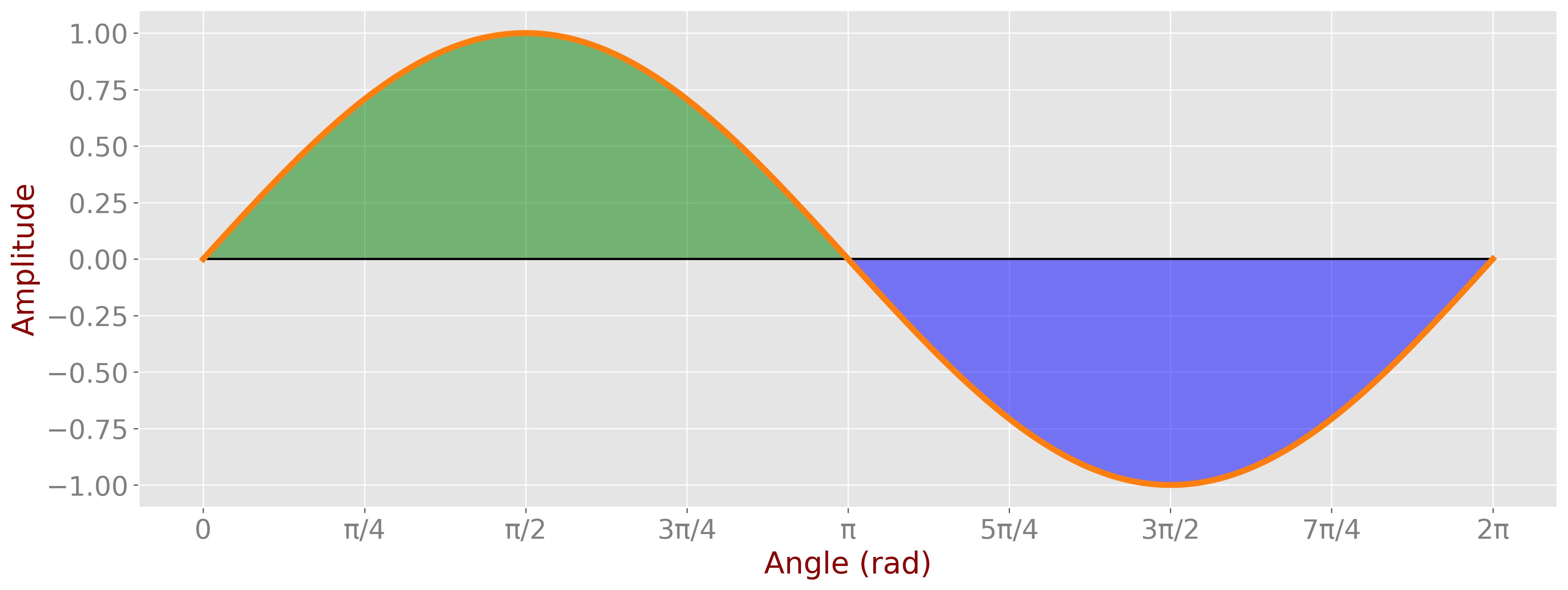
However, if \( x(t) \) has a constant component \( a_0 \), then \( \int\limits_0^T x(t) dt \) represents the area under the DC level. Dividing by \( T \) yields \( a_0 \), which is the mean of \( x(t) \).
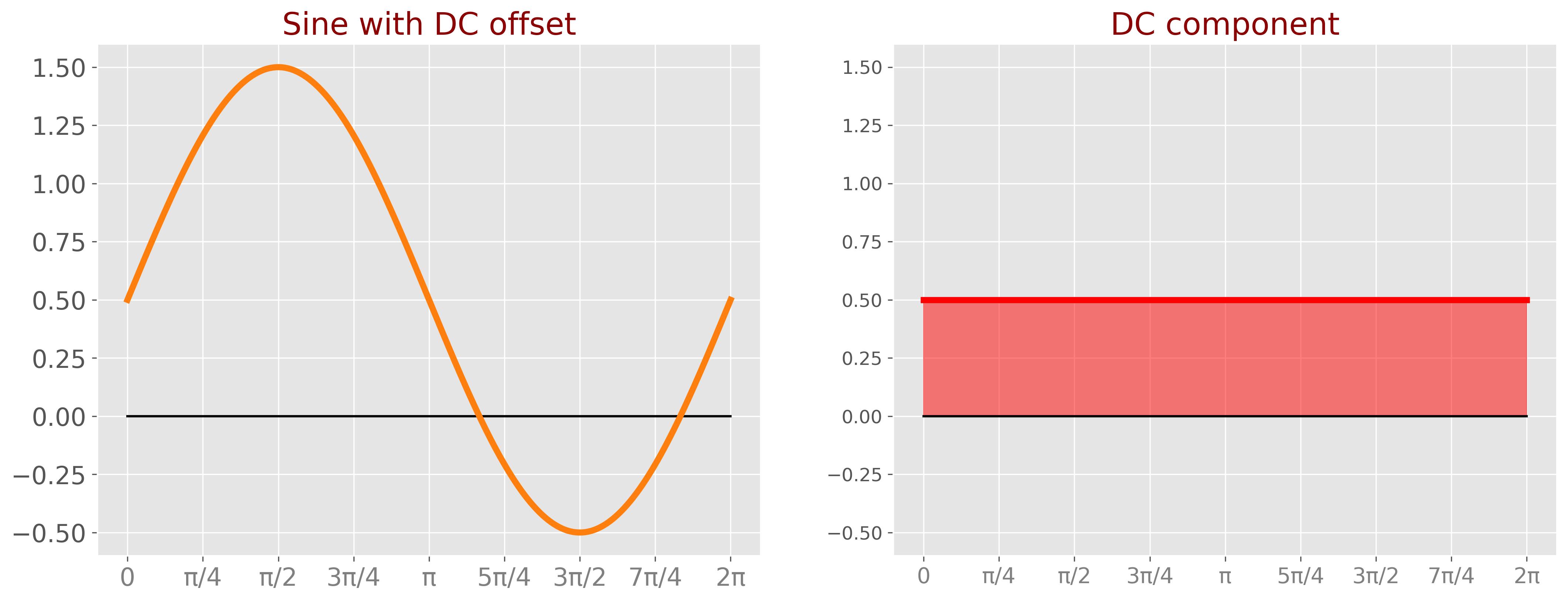
Extracting \( b_k \):
Let us find the correlation between \( x(t) \) and any given \( \sin(\omega_k t) \):
\[ \int\limits_0^T x(t) \sin(\omega_k t) dt = \int\limits_0^T \left( a_0 + \sum\limits_{m=1}^{M} \left( b_m \sin(\omega_m t) + a_m \cos(\omega_m t) \right) \right) \sin(\omega_k t) dt \]Expanding this, we get:
\[ \color{green}{a_0 \int\limits_0^T \sin(\omega_k t) dt} \color{#222832}{\ +\ } \color{red}{\sum\limits_{m=1}^{M} b_m \int\limits_0^T \sin(\omega_m t) \sin(\omega_k t) dt} \color{#222832}{\ +\ } \color{blue}{\sum\limits_{m=1}^{M} a_m \int\limits_0^T \cos(\omega_m t) \sin(\omega_k t) dt} \]The first term is zero because sine is a periodic function, and its integral over a full period \( T \) equals zero.
\[ \color{green}{a_0 \int\limits_0^T \sin(\omega_k t) dt = -a_0 \frac{1}{\omega_k} \left[ \cos(\omega_k t) \right]_0^T = -a_0 \frac{1}{\omega_k} (1-1) = 0} \]The third term also yields zero based on orthogonality properties (as shown in Appendix B):
\[ \color{blue}{\int\limits_0^T \cos(\omega_m t) \sin(\omega_k t) dt = 0} \]For the second term, we use the identity (as shown in Appendix B):
\[ \int\limits_0^T \sin(m\omega t) \sin(n\omega t) dt = \begin{cases} 0, & m \neq n \\ \frac{T}{2}, & m = n \end{cases} \]Therefore:
\[ \color{red}{\int\limits_0^T \sin(\omega_m t) \sin(\omega_k t) dt = 0, \quad \text{for } \omega_m \neq \omega_k} \] \[ \color{red}{\int\limits_0^T \sin(\omega_m t) \sin(\omega_k t) dt = \frac{T}{2}, \quad \text{for } \omega_m = \omega_k} \]Based on the above:
\[ \int\limits_0^T x(t) \sin(\omega_k t) dt = b_k \frac{T}{2} \]Solving for \( b_k \):
The Fourier Coefficient \( b_k \) equals the correlation between \( x(t) \) and \( \sin(\omega_k t) \) normalized by \( T/2 \).
Extracting \( a_k \):
Let us find the correlation between \( x(t) \) and any given \( \cos(\omega_k t) \):
\[ \int\limits_0^T x(t) \cos(\omega_k t) dt = \int\limits_0^T \left( a_0 + \sum\limits_{m=1}^{M} \left( b_m \sin(\omega_m t) + a_m \cos(\omega_m t) \right) \right) \cos(\omega_k t) dt \]Expanding this, we get:
\[ \color{green}{a_0 \int\limits_0^T \cos(\omega_k t) dt} \color{#222832}{\ +\ } \color{red}{\sum\limits_{m=1}^{M} b_m \int\limits_0^T \sin(\omega_m t) \cos(\omega_k t) dt} \color{#222832}{\ +\ } \color{blue}{\sum\limits_{m=1}^{M} a_m \int\limits_0^T \cos(\omega_m t) \cos(\omega_k t) dt} \]The first term is zero because cosine is a periodic function, and its integral over a full period \( T \) equals zero.
\[ \color{green}{a_0 \int\limits_0^T \cos(\omega_k t) dt = a_0 \frac{1}{\omega_k} \left[ \sin(\omega_k t) \right]_0^T = a_0 \frac{1}{\omega_k} (0-0) = 0} \]The second term also yields zero based on orthogonality properties (as shown in Appendix B):
\[ \color{red}{\int\limits_0^T \sin(\omega_m t) \cos(\omega_k t) dt = 0} \]For the third term, we use the identity (as shown in Appendix B):
\[ \int\limits_0^T \cos(m\omega t) \cos(n\omega t) dt = \begin{cases} 0, & m \neq n \\ \frac{T}{2}, & m = n \end{cases} \]Therefore:
\[ \color{blue}{\int\limits_0^T \cos(\omega_m t) \cos(\omega_k t) dt = 0, \quad \text{for } \omega_m \neq \omega_k} \] \[ \color{blue}{\int\limits_0^T \cos(\omega_m t) \cos(\omega_k t) dt = \frac{T}{2}, \quad \text{for } \omega_m = \omega_k} \]Based on the above:
\[ \int\limits_0^T x(t) \cos(\omega_k t) dt = a_k \frac{T}{2} \]Solving for \( a_k \):
The Fourier Coefficient \( a_k \) equals the correlation between \( x(t) \) and \( \cos(\omega_k t) \) normalized by \( \frac{2}{T} \).
Scaling
The Fourier coefficients are defined as:
In many texts, these coefficients are instead expressed as:
As discussed in the Essential Background chapter, the ratio between angle and time for sine or cosine functions remains constant and is equal to the angular frequency \( \omega \):
Thus, integrating over the interval \( [0,T] \) and normalizing by \( T \) is equivalent to integrating over \( [0,2\pi] \) and normalizing by \( 2\pi \). Since we are working with periodic functions, the integral limits can also be chosen as \( [-T/2,T/2] \) or \( [-\pi,\pi] \) without affecting the results.