Fourier Analysis of periodic signals#

Fourier analysis is a fundamental mathematical method used to analyze and represent signals by breaking them down into frequency components. It decomposes a function or signal into combinations of simple sinusoids - sines and cosines. This decomposition provides valuable insights into the signal's frequency content and behavior, making it a powerful tool in signal processing, communication systems, and physics.

This chapter focuses on the Fourier analysis of continuous periodic or continuous time-limited signals using the Fourier Series.

The Fourier Series is a theoretical tool for the spectral analysis of continuous periodic signals. Its discrete counterpart, the Discrete Fourier Transform (DFT), is used to analyze discrete periodic signals. The DFT is a practical tool widely employed for the spectral analysis of arbitrarily sampled signals. I will delve into the DFT after discussing the sampling process. We will focus on the Fourier Series, as it provides the theoretical foundation for understanding spectral analysis.

Periodic functions definition#

A periodic signal is a signal that repeats itself at regular intervals over time. Mathematically, a signal \( x(t) \) is periodic if there exists a positive constant \( T \), known as the period, such that:

                                                \[
                                                x(t) = x(t+T), \quad \text{for all } t
                                                \]
                                            

For discrete signals \( x[n] \), the signal is periodic if there exists a positive integer \( N \) such that:

                                                \[
                                                x[n] = x[n+N], \quad \text{for all } n
                                                \]
                                            

A signal is classified as aperiodic if it does not meet these conditions.

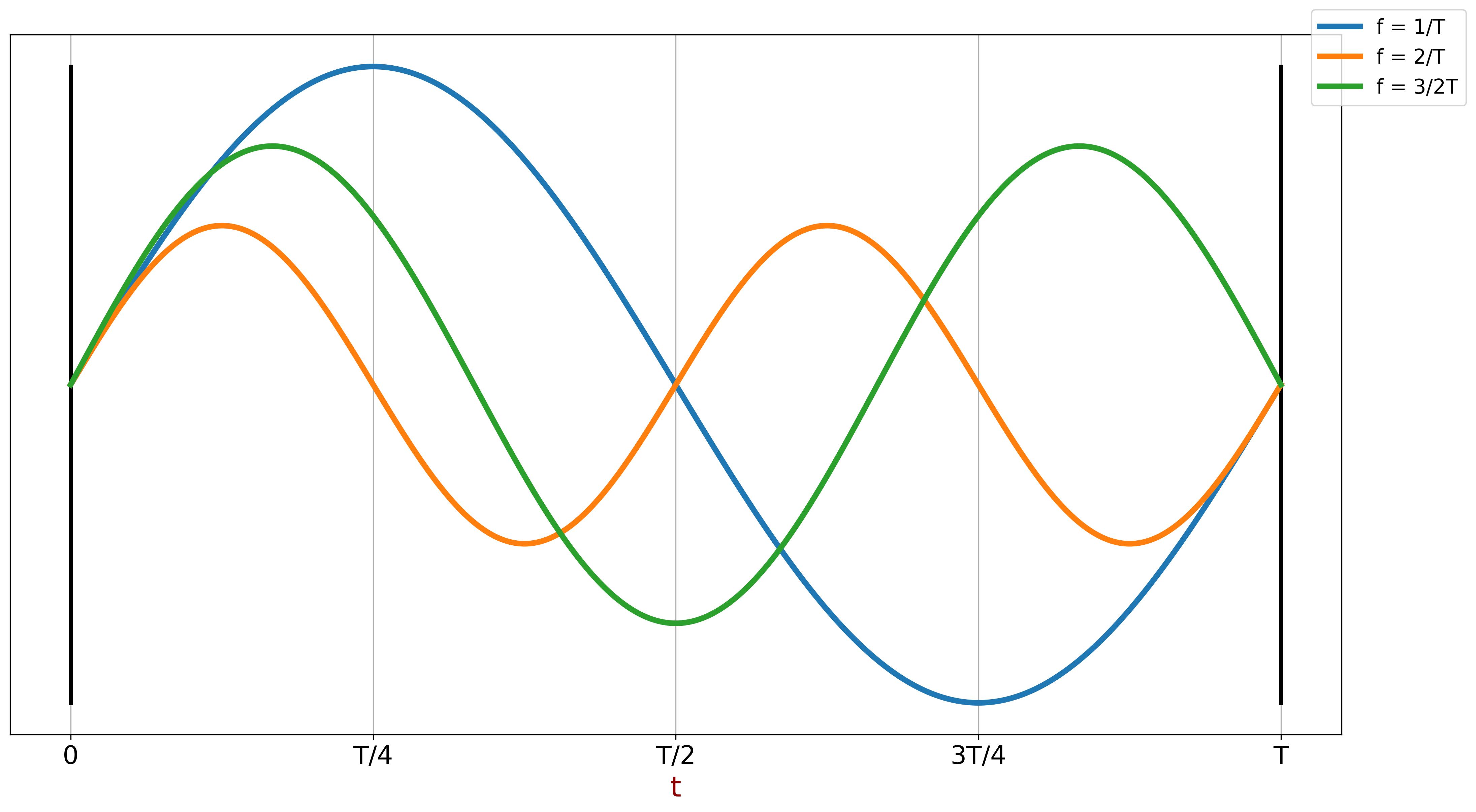
The fundamental frequency of a periodic signal is given by \( f_0 = \dfrac{1}{T} \). Additionally, sine functions with frequencies that are integer multiples of \( f_0 \) (i.e. \( mf_0 \) for \( m \in \mathbb{Z} \)) remain periodic over period \( T \).

The following figure illustrates examples of periodic and aperiodic sine functions. Notice that the green sine wave is aperiodic, as it completes 1.5 cycles within the interval \( T \), meaning it does not repeat itself consistently over \( T \).

Time Limited functions definition#

A time-limited function (also called a time-bounded function or finite-duration function) is a function whose domain or support is restricted to a finite time interval. This means the function is nonzero only within a specific time range and zero (or undefined) outside that range.

\[ x(t) = 0, \quad \forall t \notin [t_1, t_2] \]

For example, a triangular window is a time-limited function.

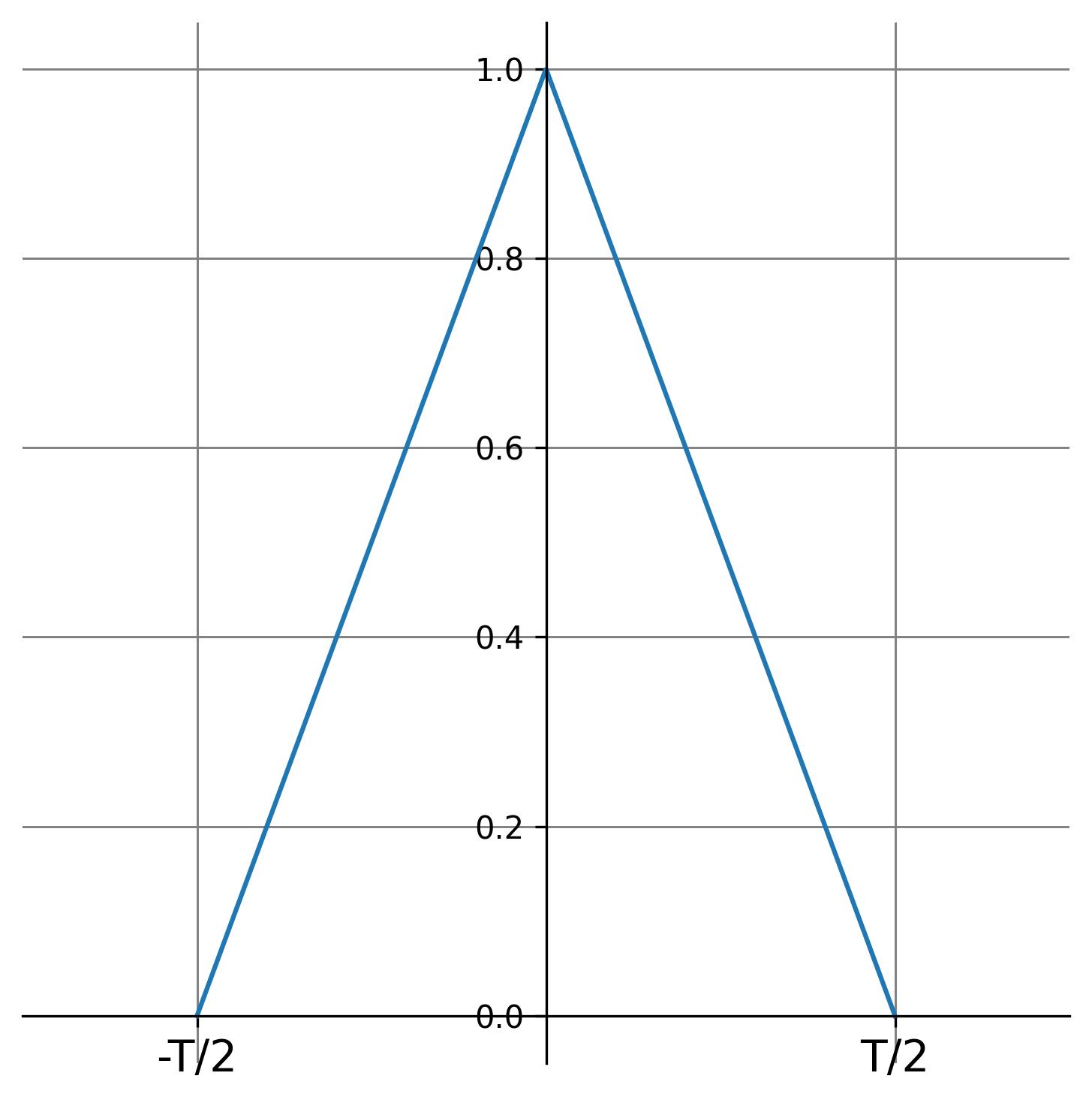
If the time-limited function \( x(t) \) is defined on \( [-T/2, T/2] \), it can be extended to a periodic function defined for all \( t \). The periodic extension of \( x(t) \) is given by:

\[ \bar{x}(t) = \begin{cases} \vdots & \\ x(t - 2T), & -\frac{5}{2}T < t < -\frac{3}{2}T \\ x(t + T), & -\frac{3}{2}T < t < -\frac{1}{2}T \\ x(t), & -\frac{T}{2} < t < \frac{T}{2} \\ x(t - T), & \frac{T}{2} < t < \frac{3}{2}T \\ x(t - 2T), & \frac{3}{2}T < t < \frac{5}{2}T \\ \vdots & \end{cases} \]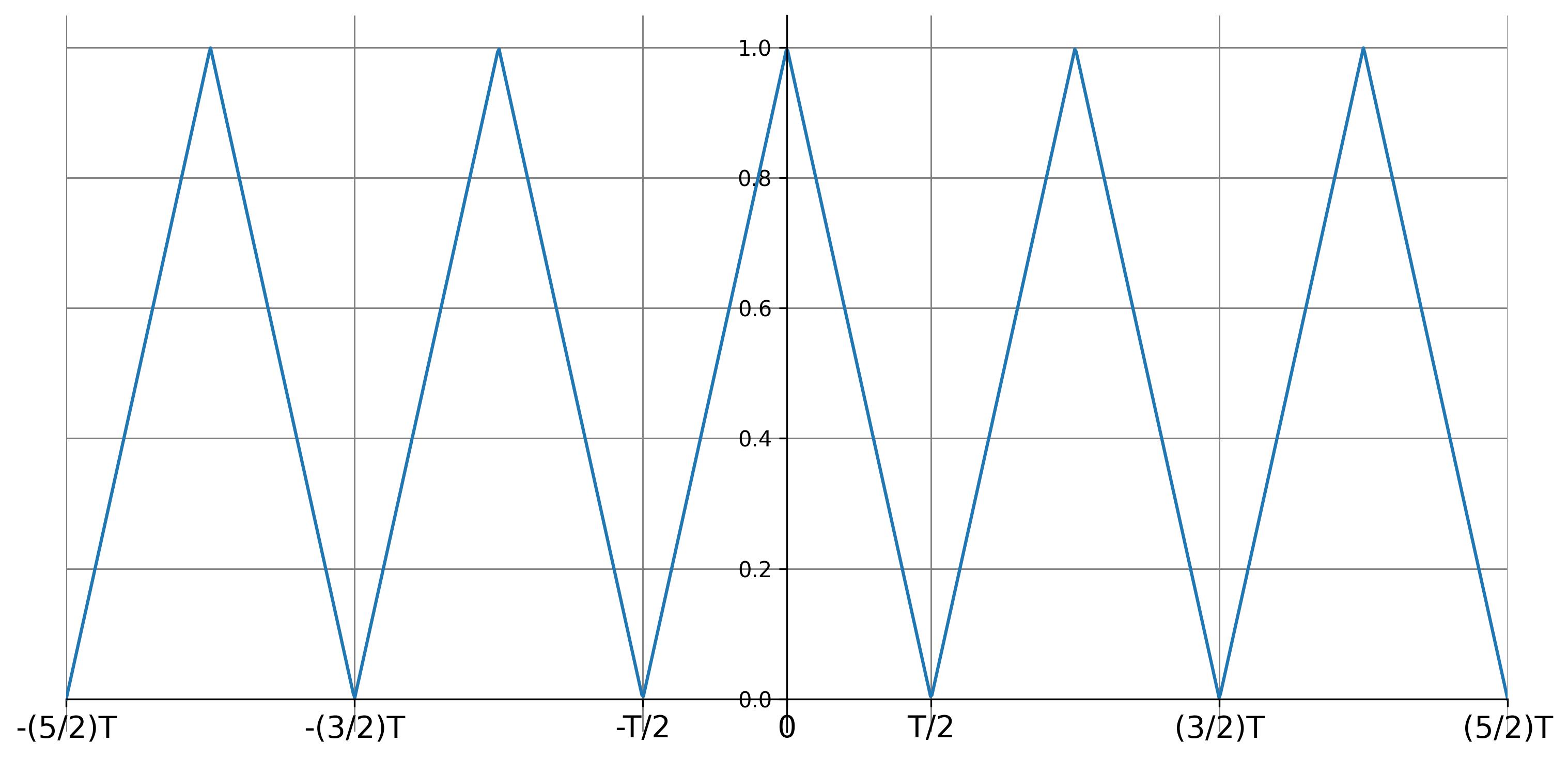

The time-limited signal can be periodic by assumption.