The idea behind Fourier Transform#
Imagine an input signal composed of \( m \) sinusoidal waves. The number \( m \) can vary, ranging from 0 to infinity. Each sinusoid is characterized by three key parameters:
- Angular Frequency (\( \omega \)): Defined as \( \omega = 2\pi f \), where \( f \) is the frequency of the sine wave.
- Amplitude (\( A \)): The height or strength of the sine wave.
- Phase Shift (\( \phi \)): The horizontal shift of the sine wave, indicating where the wave begins relative to time \( t \).
The general form of each sinusoid can be expressed as:
\[ A \sin(\omega t + \phi) \]We aim to develop an algorithm that performs spectral decomposition - breaking down the input signal to identify and extract the specific parameters (\( \omega \), \( A \), and \( \phi \)) for each sinusoid present in the input signal.
Correlation-based frequency analysis#
The Fourier Transform algorithm fundamentally relies on correlation (a measure of similarity) between an arbitrary input signal and an infinite collection of pre-defined sines and cosines, using the orthogonality property of sine and cosine functions.
By correlating the input signal with each of these stored sines and cosines, one by one, we can identify the frequencies present in the signal.
When the correlation between the input signal and a sine or cosine from the collection is nonzero, the input signal contains a sinusoidal component at the same frequency \( \omega \) as the predefined sine and cosine.
The following figure describes the concept of spectral decomposition using correlation.
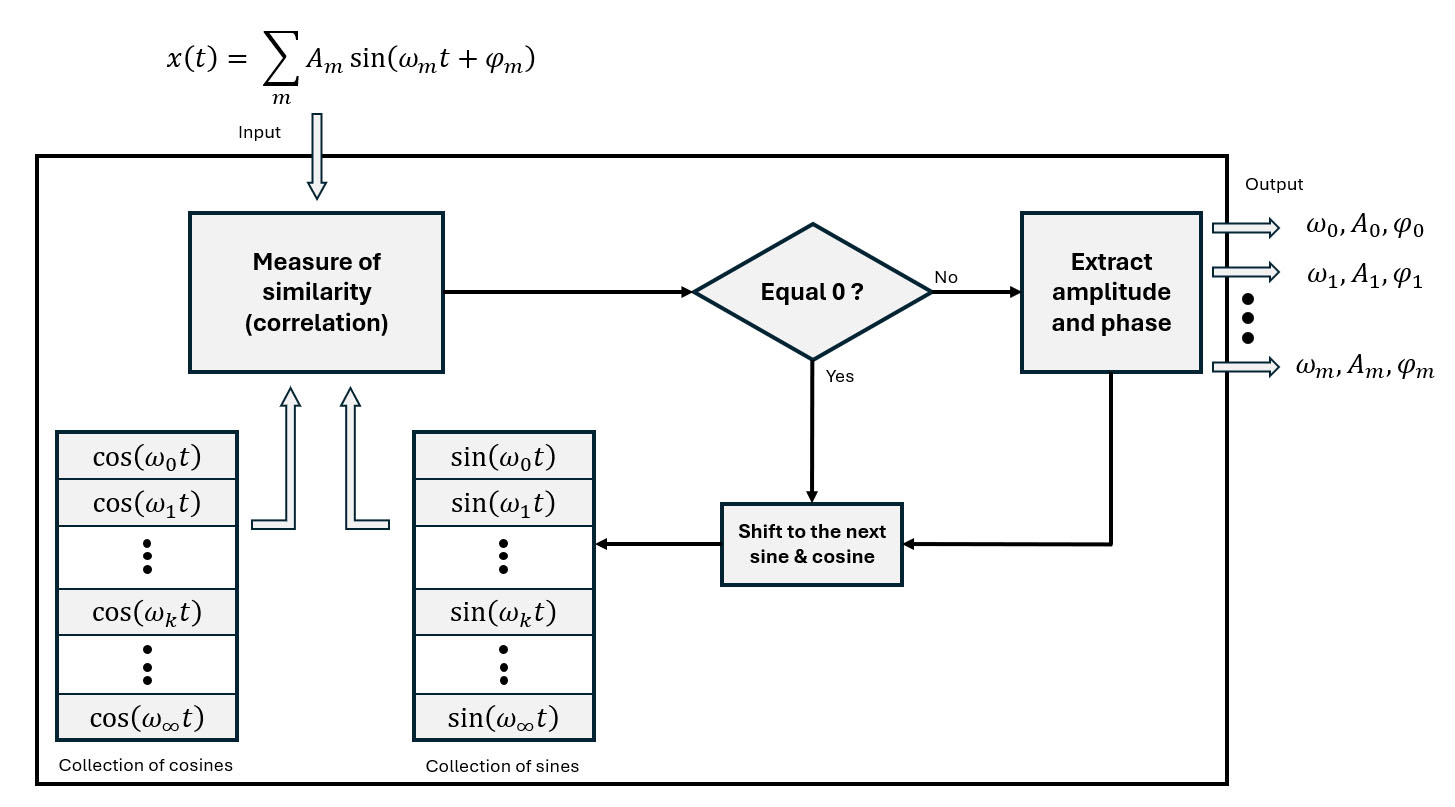
The predefined sine and cosine functions have the following frequencies:
- \(\omega_0 = 0\).
- \(\omega_1 = 2\pi f_1\), where \( f_1 = \dfrac{1}{T} \), is the fundamental frequency.
- For \( k > 1 \), the other frequencies, \( \omega_k \), are integer multiples of the fundamental frequency, ensuring periodicity within the period \( T \) (see the definition of a periodic signal).
Derivation
Let's begin with a single sinusoidal function by breaking down an arbitrary signal \( A\sin(\omega t+\phi) \) into sine and cosine components. Using the trigonometric identity:
\[ \sin(\alpha+\beta) = \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta) \]we can express the arbitrary signal as:
\[ x(t) = A\sin(\omega t+\phi) = A (\sin(\omega t)\cos(\phi) + \cos(\omega t)\sin(\phi)) \]Let us define:
\[ u = \cos(\phi), \quad v = \sin(\phi) \]We can rewrite the signal as follows:
\[ x(t) = A(u \cdot \sin(\omega t) + v \cdot \cos(\omega t)) \]This represents \( A\sin(\omega t+\phi) \) as a weighted sum of \( \sin(\omega t) \) and \( \cos(\omega t) \), where \( u \) and \( v \) are weights influenced by the phase shift \( \phi \). If \( u=0 \), then \( v=1 \) and vice versa.
The measure of similarity with \( \sin(\omega t) \)
To find a measure of similarity of the arbitrary signal with \( \sin(\omega t) \), we solve:
\[ X_C (\omega) = \int\limits_{0}^{T} A(u \cdot \sin(\omega t) + v \cdot \cos(\omega t)) \cdot \sin(\omega t) \, dt \]Expanding this gives:
\[ X_C (\omega) = A u \color{red}{\int\limits_{0}^{T} \sin^2(\omega t) \, dt} \color{#222832}{+ A v} \color{green}{\int\limits_{0}^{T} \cos(\omega t) \sin(\omega t) \, dt} \]As shown in Appendix B:
\[ \color{red}{\int\limits_{0}^{T} \sin^2(\omega t) \, dt = \frac{T}{2}} \] \[ \color{green}{\int\limits_{0}^{T} \sin(\omega t) \cos(\omega t) \, dt = 0} \]Therefore, we have:
\[ X_C (\omega) = A u \frac{T}{2} = A \frac{T}{2} \cos(\phi) \]The measure of similarity with \( \cos(\omega t) \)
To find a measure of similarity of the arbitrary signal with \( \cos(\omega t) \), we solve:
\[ X_S (\omega) = \int\limits_{0}^{T} A(u \cdot \sin(\omega t) + v \cdot \cos(\omega t)) \cdot \cos(\omega t) \, dt \]Expanding this gives:
\[ X_S (\omega) = A u \color{red}{\int\limits_{0}^{T} \sin(\omega t) \cos(\omega t) \, dt} \color{#222832}{ + A v} \color{green}{\int\limits_{0}^{T} \cos^2(\omega t) \, dt} \]As shown in Appendix B:
\[ \color{red}{\color{green}{\int\limits_{0}^{T} \cos^2(\omega t) \, dt = \frac{T}{2}}} \] \[ \int\limits_{0}^{T} \sin(\omega t) \cos(\omega t) \, dt = 0 \]Therefore, we have:
\[ X_S (\omega) = A v \frac{T}{2} = A \frac{T}{2} \sin(\phi) \]To summarize:
- The measure of similarity of the arbitrary signal \( A\sin(\omega t+\phi) \) with \( \sin(\omega t) \) is: \( X_C (\omega) = A \frac{T}{2} \cos(\phi) \).
- The measure of similarity of the arbitrary signal \( A\sin(\omega t+\phi) \) with \( \cos(\omega t) \) is: \( X_S (\omega) = A \frac{T}{2} \sin(\phi) \).
Extracting the phase \( \phi \)
\[ \frac{X_S (\omega)}{X_C (\omega)} = \frac{A \dfrac{T}{2} \sin(\phi)}{A \dfrac{T}{2} \cos(\phi)} = \frac{\sin(\phi)}{\cos(\phi)} = \tan(\phi) \]Extracting the amplitude \( A \)
\[ \sqrt{(X_C (\omega))^2 + (X_S (\omega))^2} = \sqrt{\left(A \frac{T}{2} \cos(\phi) \right)^2 + \left(A \frac{T}{2} \sin(\phi) \right)^2} \] \[ = A \frac{T}{2} \sqrt{\sin^2(\phi) + \cos^2(\phi)} \] \[ = A \frac{T}{2} \]Therefore, solving for \( A \):
Summary
The amplitude \( A \) and the phase \( \phi \) of the arbitrary signal with frequency \( \omega \) can be determined by calculating the measure of similarity between the input signal and functions \( \sin(\omega t) \) and \( \cos(\omega t) \).
- If \( u=0 \), then the input signal is a pure cosine.
- If \( v=0 \), then the input signal is a pure sine.
A brief note on notation:
- A signal in the time domain is represented by a lowercase letter, \( x(t) \), while its corresponding representation in the frequency domain is denoted by an uppercase letter, \( X(\omega) \).
- Subscripts \( C \) and \( S \) represent the cosine and sine components of the signal, respectively.