Introduction
What is Fourier Transform#
A few years ago, I was watching a culinary competition on TV. The contestants had to taste a soup containing more than twenty ingredients and identify them. The winner, impressively, managed to determine every single ingredient.

We can think of this process in a systematic way. The soup is like an input signal. The tongue acts as a sensor, converting the signal into electrical impulses that travel through the nervous system (the wires) to the brain (the CPU). The brain runs an algorithm that distinguishes between different signal components corresponding to individual ingredients.
This mental process is similar to what the Fourier Transform does. Just as the contestant identified distinct flavors within a complex mixture, the Fourier Transform decomposes a complex signal into its fundamental frequency components.
Consider the following figure:
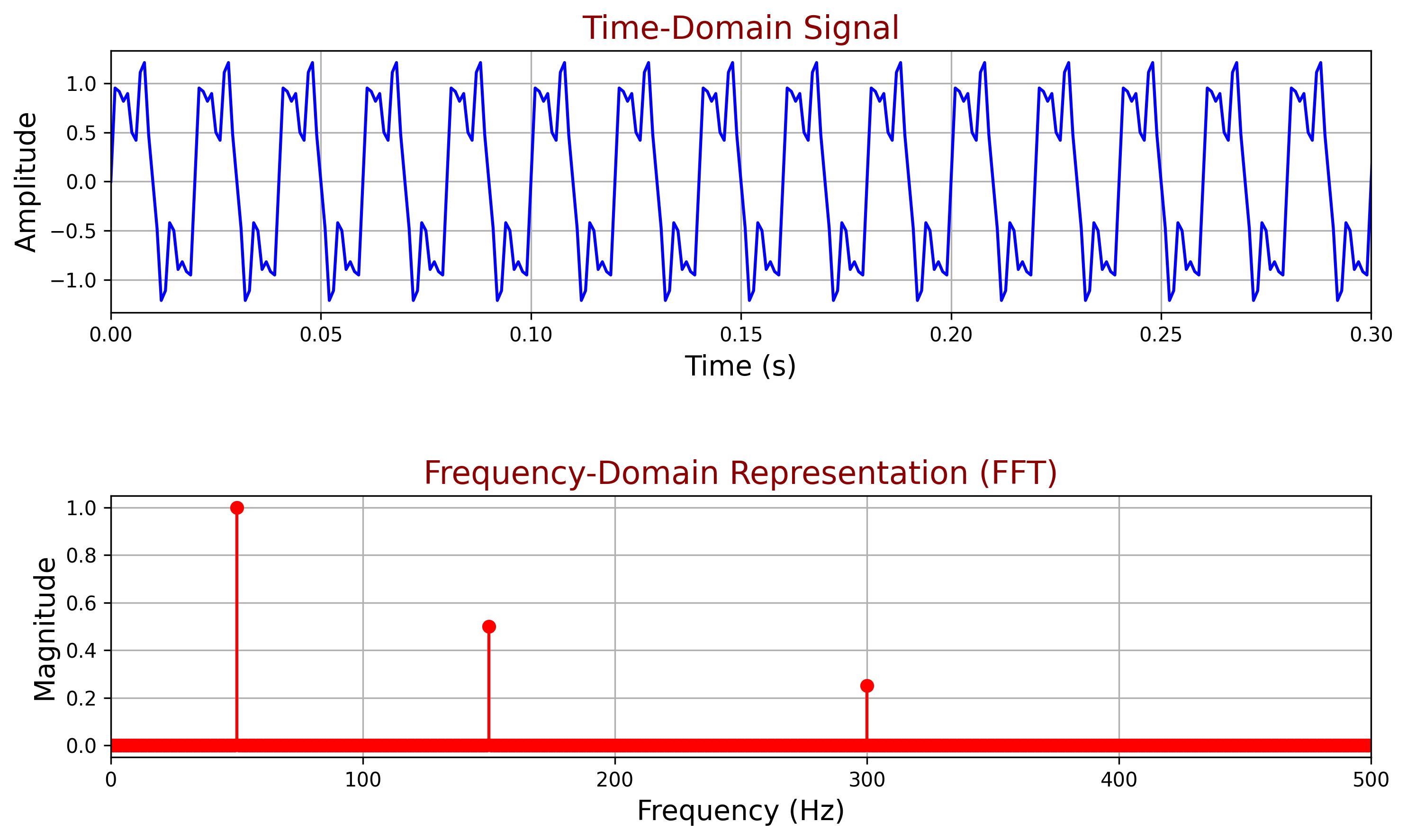
The upper plot represents a signal in the time domain composed of three sinusoidal waves. Simply looking at it makes it difficult to tell what frequencies make up the signal. This is where the Fourier Transform comes in. The lower plot shows the Fourier Transform output, revealing the signal’s frequency components and their magnitudes - essentially, its "ingredients."
The Fourier Transform is one of the most powerful tools in science and engineering. It plays a fundamental role in telecommunications (radio, television, mobile networks, GPS), medical imaging (MRI, CT scans), audio and music processing, image analysis, astronomy, finance, artificial intelligence, and many other fields.
About this tutorial#
The Fourier Transform is widely used in digital signal processing. Yet, throughout my career, I’ve noticed that many engineers, despite using it regularly, don’t fully understand how it works.
My name is Alex Becker, and I’m an engineer with over 20 years of experience in systems engineering and signal processing. Over time, I’ve developed a skill for breaking down complex topics into simpler terms, making them easier to grasp. This inspired me to create an online tutorial dedicated to the Fourier Transform. You can also check out my online tutorial on Kalman Filtering at www.kalmanfilter.net.
This tutorial focuses on the practical aspects of the Fourier Transform while also providing the necessary mathematical foundation. By the end, you’ll not only use it confidently but also understand exactly what the famous Fourier Transform equation
actually does. You’ll also be able to compute the Fourier Transform by hand, using pen and paper, and implement it in Python, MATLAB, and C.
Jean-Baptiste Joseph Fourier#
Joseph Fourier (1768–1830) was a French mathematician and physicist best known for developing the Fourier Transform and Fourier Series. His groundbreaking work on heat transfer led to the discovery that functions can be represented as sums of sinusoids - an idea that remains fundamental in modern science and technology.

Joseph Fourier's life is fascinating, marked by significant contributions to mathematics, physics, and even Egyptology. For a more in-depth look at his biography, you can explore the following resources:
Real or complex Fourier Transform?#
You are likely familiar with the well-known Fourier Transform equation:
\[ X(\omega) = \int\limits_{-\infty}^{\infty} x(t) e^{-i\omega t} \,dt \]
This equation represents a measure of similarity between the input signal \( x(t) \) and a complex sinusoid \( e^{-iωt} \). The result of this computation is the frequency component of \( x(t) \) at frequency \(\omega \).
However, understanding the Fourier Transform does not require prior knowledge of complex numbers. The same fundamental operation can be performed using only real numbers, leading to an equivalent result. The real Fourier Transform expresses a signal in terms of real-valued cosine and sine components.
Personally, I prefer the complex representation for its elegance, compactness, and convenience in mathematical derivations. However, the real Fourier Transform provides a more accessible introduction, making it easier to grasp the underlying concepts.
For this reason, we will begin our discussion using real numbers. Once the core ideas of Fourier Transform are well understood, we will transition to the complex form. Don’t worry - I will introduce complex numbers along the way, making the transition straightforward.